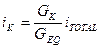Answer: A.
84. What formula expresses correctly the voltage division rule application for k-th resistor if k of them are connected in series? A. vk=vtotal*(Req/Rk) B.vk=vtotal*(Rk/Req) C. vk=vtotal*(R1/Req) D. vk=vtotal/(Rk/Req) E. vk=vtotal*(Rk-1/Req) Solution:
The Voltage Division Rule for k-th resistor if k of them are connected in series is Answer: B.
(between points A and D) A.0.5R B.R C.1.5R D.2R E.3R
Solution: 1st way
This gives 2R/3+R/3=R. Answer: B. D way Points B and C are symmetrical respectively to points A and D, so potential of point B equals to potential of point C. Then we can ignore resistor between points B and C. As a result, we have got the circuit, where four resistors of R are connected in two groups of R/2 (two resistors of R in parallel). So resultant value of Req=R/2+R/2=R 86. What formula expresses correctly the current division rule application for k-th resistor if k of them are connected in parallel? A. ik=itotal*(Req/Rk) B.ik=itotal*(Rk/Req) C. ik=itotal*(R1/Req) D. ik=itotal*(Gk/Geq) E. ik=itotal*(Geq/Gk)
Solution: The current division rule for k-th resistor if k of them are connected in parallel is
|
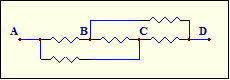85. What is the equivalent resistance for the circuit below if all resistances are equal to R?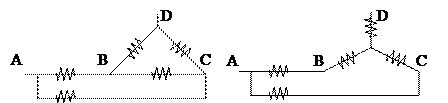
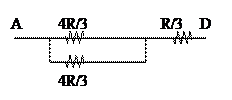The values of star sides will be three times less, that is R/3, so after reducing resistors in series there will be parallel combination of two resistors with values 4R/3 (R+R/3) in series with one R/3 resistor.
