Дія магнітного поля на рухомий електричний заряд. Сила Ампера і сила Лоренца
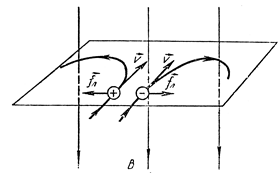
Силова дія магнітного поля на провідник зі струмом визначається відповідно до емпіричного закону Ампера (1820 р.): FА = I × B × dl ×sin a, (4.50) де a – кут, утворений векторами dl і B. Сила АмпераFA діє на провідник зі струмом в магнітному полі. Вона є результатом дії магнітного поля на рухомі електричні заряди, котрі створюють даний електричний струм I. Сила fл, яка діє на окремий рухомий заряд, називається силою Лоренца і може бути визначена із співвідношення:
де N = n×V = n×dl×S – загальна кількість вільних носіїв заряду в провіднику. Враховуючи, що I = j×S,а j = q 0 nυ;, отримаємо вираз для сили Лоренца, що діє з боку магнітного поля на окремий електричний заряд q 0, який рухається зі швидкістю υ;: fл = q 0× υ;× B ×sin a, (4.51) де a – кут між векторами υ; і B. Напрям сили Лоренца визначається, як і напрям сили Ампера, за правилом свердлика i залежить від знаку заряда (мал. 4.20). Оскільки сила Лоренца перпендикулярна до площини, в якій лежать вектори υ; і B, то ця сила надає частинці доцентрового прискорення. Припустимо, що заряджена частинка q 0 влітає з швидкістю υ; в однорідне магнітне поле B перпендикулярно до силових ліній, тоді відповідно до другого закону Ньютона mυ;2 /R = q 0× υ;× B. (4.52) Звідси Період обертання T =
|
,
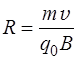– радіус кола, по якому рухається частинка.
= 
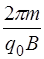. (4.53)
