Динамическая остойчивость судна
Динамической остойчивостью называется способность судна противостоять, не опрокидываясь, динамическому воздействию внешних моментов. До сих пор при рассмотрении вопросов остойчивости предполагалось, что кренящий момент действует на судно статически, т.е. кренящий момент mкр был равен восстанавливающему моменту mΘ. Это могло быть:
1) либо при столь медленном нарастании mкр, что в любой момент осуществлялось равенство mкр = mΘ; 2) либо в положении судна, когда с момента mкр приложения прошло достаточно много времени. В действительности во многих случаях кренящий момент прикладывается к судну динамически (накат волны, шквальный ветер и т.п.). В этих случаях нарастание кренящего момента происходит быстрее, чем восстанавливающий момент и равенство между моментами не соблюдается. В результате процесс наклонения судна совершается с ускорением. Наибольший угол крена, которого достигает судно при наклонении с ускорением, называется динамическим углом крена Θдин. Величина Θдин значительно превышает величину статического угла крена Θс (при mкр.дин = mкр.ст). Возможен случай, когда при значительном угловом ускорении величина Θдин окажется настолько большой, что судно опрокинется (при неопасном для судна статическом приложении равного по величине mкр).
В теории судна при изучении динамических наклонений обычно делается допущение, что вода и воздух не оказывают сопротивления такому наклонению; это допущение привод к погрешности в безопасную сторону.
Рис.62. К рассмотрению динамических наклонений
6.3.1. Наклонение судна при динамическом воздействии кренящего момента. Предположим, что к судну, имеющему Θ = 0, динамически приложен момент mкр, который затем продолжает дей-
ствовать статически, не изменяясь по величине с изменением угла крена Θ (рис.62). На участке наклонения судна от Θ = 0 до Θст, когда mкр > mΘ, происходит накопление кинетической энергии за счет избыточной работы кренящего момента, угловая скорость растет dΘ/dt, угловое ускорение d2Θ/dt2 положительное, но величина его уменьшается вследствие противодействия восстанавливающего момента. При Θ = Θст, когда mкр = mΘ, скорость наклонения судна и кинетическая энергия достигают максимальных значений, а ускорение равно нулю. На участке наклонения судна от Θст до Θдин, когда mкр < mΘ, накопленная ранее кинетическая энергия погашается противоположной по знаку избыточной работой восстанавливающего момента, скорость наклонения уменьшается, ускорение отрицательное и с нарастанием угла Θ величина его растет. Наклонение судна прекращается в точке Θдин, в которой наблюдается равенство работ кренящего Акр и восстанавливающего моментов АΘ. Эти работы можно записать как
Положение судна с Θ = Θдин не является положением равновесия. Под действием избыточного восстанавливающего момента судно начнет спрямляться (до Θ = Θст ускоренно, а затем замедленно) и придет в положение Θ = 0 (при отсутствии сил сопротивления) с нулевой угловой скоростью. После этого явление повторяется - судно будет колебаться около положения Θ = Θст. При отсутствии сопротивления этим колебаниям со стороны воды и воздуха они могли бы продолжаться бесконечно. В действительности судно совершает в рассматриваемом случае затухающие колебания и в итоге останавливается в положении равновесия с углом Θст. Рис.63. К определению динамических углов крена судна.
6.3.2. Определение динамического угла крена судна. Запас динамической остойчивости. Величину угла Θдин при воздействии на судно момента mкр заданной величины можно найти с помощью равенства работ Акр = АΘ при наклоне Θ = Θдин
или или Где интеграл На рис. 63 работа кренящего момента Акр представляет собой прямоугольник ОКВD, а работа восстанавливающего момента АΘ криволинейную трапецию ОАМВD. Заштрихованные площади 1(ОКА) и 2 (АМВ) соответствуют избыточным работам кренящего δАкр и восстанавливающего моментов δАΘ. Следовательно, угол Θдин может быть определен по диаграмме статической остойчивости графически из условия равенства по величине площадей 1 и 2. Как видно из рис.63, при типичном виде диаграммы статической остойчивости Θдин» 2 Θст. Из сказанного выше очевидно, что работа восстанавливающего момента может служить мерой динамической остойчивости судна. Площадь на ДСО под кривой mΘ (Θ) ОАМВN (на рис.63), характеризующую собой работу АΘ, называют запасом динамической остойчивости судна (ЗДО). Чем больше эта площадь, тем большей динамической остойчивостью обладает судно при плавании в прямом положении. При рассмотрении рисунка 55, становится очевидным, что чем меньше метацентрическая высота судна, тем меньше не только запас статической остойчивости, но и динамической. При плавании судна
со статическим углом крена Θст.1 запас динамической остойчивости уменьшается и на рисунке 63 он определяется только площадью АМВ между кривой mΘ (Θ) и mкр(Θ). 6.3.3. Пределы динамической остойчивости судна. Такими пределами являются: - максимальный кренящий момент mкр.дин.max, динамическое приложение которого еще не вызывает опрокидывание судна (опрокидывающий момент); - максимальный динамический угол крена Θдин.max. Для нахождения величин mкр.дин.max и Θдин.max можно использовать диаграмму статической остойчивости (рис.63). По мере увеличения mкр. угол Θдин растет. При некотором mкр. = mкр.дин.max, что соответствует предельному случаю равенства площадей 1 и 2, когда еще может быть обеспечено равенство избыточных работ восстанавливающего и кренящего моментов, угол Θдин = Θдин.max. Следовательно, Θдин.max определяется точкой пересечения графика mкр(Θ), отвечающего mкр.дин.max, с нисходящей ветвью ДСО. Если при динамическом приложении кренящего момента его величина mкр > mкр.дин.max, то избыточная работа кренящего момента уже не может быть полностью погашена избыточной работой восстанавливающего момента, и судно опрокинется. При статическом приложении такого же по величине момента mкр безопасность плавания судна обеспечивается, если только mкр £ mкр.ст.max. Из рис.63 видно, что mкр.дин.max < mкр.ст.max. Таким образом, динамическая остойчивость судна при воздействии mкр заданной величины обеспечена, если динамический угол крена не превосходит значения, при котором работа кренящего момента еще может быть компенсирована работой восстанавливающего момента. 6.3.4. Диаграмма динамической остойчивости судна. Для решения задач динамической остойчивости удобно использовать диаграмму динамической остойчивости (ДДО), которая определяет работу восстанавливающего момента АΘ при каждом значении угла Θ (рис.64). Как известно, работа восстанавливающего момента по углу крена может быть представлена выражением АΘ =
где функция mΘ(Θ) представляет собой диаграмму статической остойчивости (ДСО).
Рис.64. Диаграмма динамической остойчивости
Таким образом, ДДО является интегральной кривой по отношению к ДСО. Как всякая интегральная кривая, она обладает следующими свойствами: 1) каждая ее ордината выражает собой площадь под ДСО по эту ординату; 2) точка перегиба (точка В) соответствует максимуму ДСО; 3) максимум интегральной кривой (точка С) соответствует углу заката ДСО; 4) ордината ДДО при Θ = Θзак определяет собой запас динамической остойчивости судна в прямом положении равновесия; 5) тангенс угла касательной, проведенной к диаграмме динамической остойчивости, определяет ординату диаграммы статической остойчивости при том же угле крена. Так как mΘ = γV lΘ , то выражение для работы восстанавливающего момента можно записать в виде АΘ = где
Таким образом, при равнообъемных наклонениях судна (V = const) ДДО может быть построена не только для работы восстанавливающего момента АΘ, но и для плеча динамической остойчивости lдин. Масштабы при этом выбираются таким образом, чтобы одна кривая выражала как АΘ (Θ) так и lдин(Θ).
Рис.65. Диаграммы динамической остойчивости судна: а – с положительной остойчивость; б – с отрицательной остойчивостью
С помощью ДДО легко определить Θдин от динамического воздействия на судно кренящего момента mкр, а также пределы динамической остойчивости судна mкр.дин.max и Θдин.max. При условии, что величина mкр не изменяется с изменением угла крена, работа кренящего момента
и график Акр(Θ) выражается прямой, проведенной из начала координат (рис. 65,а). Для построения этого графика при Θ = 1 рад проводят вертикаль, на ней откладывается в масштабе работ величина mкр (отрезок DЕ) и из начала координат через точку D проводится искомая прямая. Точка пересечения графиков Акр(Θ) и АΘ (Θ) определяет величину угла Θдин, так как при этом выполняется равенство Акр = АΘ.
Предельные касательные, проведенные параллельно прямой ОD к диаграмме динамической остойчивости, определяют статические углы крена Θ1 и Θ2.
Рис.66. Определение опрокидывающего момента: а) – для судна плавающего прямо (Θ0 = 0); б) – для судна с отрицательной начальной остойчивостью; в) – для судна, наклоненного на угол Θ0; г) – для судна с начальным креном Θ0 вследствие смещения ЦТ от ДП.
На рисунке 66 рассмотрено определение пределов динамической остойчивости судна для типичных случаев.
Для определения mкр.дин.max и Θдин.max для судна находящегося в прямом положении (Θ = 0), из начала координат к ДДО проводится касательная (рис.66,а). Очевидно, что эта касательная является графиком Акр = (mкр.дин.max) Θ. Абсцисса точки касательной определит величину угла Θдин.max. Ордината касательной при Θ = 1 рад выражает в масштабе работ величину опрокидывающего момента mопр=mкр.дин.max.
|




 (mкр – mΘ) dΘ = 0,
(mкр – mΘ) dΘ = 0,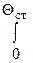 (mкр – mΘ) dΘ +
(mкр – mΘ) dΘ +  (mкр – mΘ) dΘ = 0
(mкр – mΘ) dΘ = 0








