ОбщезначимостьФормула (исчисления предикатов) общезначима, если она истинна в любой интерпретации. Теорема 4.14. Формула Доказательство. Рассмотрим произвольную интерпретацию I, произвольную последовательность значений из области интерпретации s и соответствующую функцию Пусть А(х) — формула, а терм t свободен для х в А. Положим A(t)=A(...x...){t//x}. Имеем: Можно также показать, что формула A(t) О полноте чистого исчисления предикатов Существуют с ледующие две метатеоремы, которые устанавливают свойства исчисления предикатов, аналогичные тем, которые установлены для исчисления высказываний в подразделе 4.3. Теоремы приводим без доказательств. Теорема 4.15. Всякая теорема чистого исчисления предикатов первого порядка общезначима. Теорема 4.16. Всякая общезначимая формула является теоремой чистого исчисления предикатов первого порядка.
|
x А(х) 
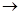A(t), где терм t свободен для переменной х в формуле А, общезначима.
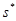. Пусть 
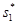(t'), где s 1 имеет значение а 1 на месте х.
x A(x), где терм t свободен для переменной x в формуле А, общезначима.
