Доказательство (Для случая L.) Г, ┐S├ F Г &┐S F - тавтология. Но
Г &┐ S Имеем: Г Пустая формула не имеет никакого значения ни в какой интерпретации, в частности, не является истинной ни в какой интерпретации и, по определению, является противоречием. В качестве формулы F при доказательстве от противного по методу резолюций принято использовать пустую формулу. Метод резолюций работает с особой стандартной формой формул, которые называются предложениями. Предложение — это бескванторная дизъюнкция литералов. Любая формула исчисления предикатов может быть преобразована в множество предложений следующим образом (здесь знак
1. Элиминация импликации. Преобразование: А 2. Протаскивание отрицаний. Преобразования: ┐ 3. Разделение связанных переменных. Преобразование: Q 1 x A(... Q 2 x B(... x...)...) где Q 1 и Q 2 — любые кванторы. После третьего этапа формула не содержит случайно совпадающих связанных переменных. 4. Приведение к предваренной форме. Преобразования: Q x A где Q — любой квантор. После четвертого этапа формула находится в предваренной форме. 5. Элиминация кванторов существования (сколемизация). Преобразования:
где а — новая предметная константа, f — новый функтор, a Q 1, Q 2,..., Qn — любые кванторы. После пятого этапа формула содержит только кванторы всеобщности. 6. Элиминация кванторов всеобщности. Преобразование: 7. Приведение к конъюнктивной нормальной форме. Преобразование: A После седьмого этапа формула находится в конъюнктивной нормальной форме. 8. Элиминация конъюнкции. Преобразование: A&В Не все преобразования на этапах 1-8 являются логически эквивалентными. Теорема 4.21. Если Г — множество предложений, полученных из формулы S, то S является противоречием тогда и только тогда, когда множество Г невыполнимо. Доказательство. В доказательстве нуждается шаг 5 — сколемизация. Пусть F= Положим F': = xi+1,...,xn). Пусть F — противоречие, a F' — не противоречие. Тогда существует интерпретация I и набор значений s = (a 1,..., ai- 1, ai+ 1,..., an) такой что
Множество формул Г невыполнимо — это означает, что множество Г не имеет модели, то есть не существует интерпретации, в которой все формулы Г имели бы значение И.
|

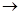 F = ┐(Г&┐ S)
F = ┐(Г&┐ S)  F = ┐(Г&┐ S) = ┐Г
F = ┐(Г&┐ S) = ┐Г 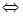 Г ├ S.
Г ├ S.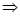 используется для обозначения способа преобразования формул).
используется для обозначения способа преобразования формул). ,
,  .
.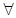 x 1 ...
x 1 ... 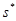 (F') = И. Положим ai:= f(a 1,..., ai- 1 ), s 1:= (a 1,..., ai- 1, ai, ai+ 1,..., an). Тогда
(F') = И. Положим ai:= f(a 1,..., ai- 1 ), s 1:= (a 1,..., ai- 1, ai, ai+ 1,..., an). Тогда 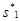 (F) = И и F — выполнимая формула.
(F) = И и F — выполнимая формула.


