Задачи и упражнения. 2. Описать процедуру, которая перечисляет множество термов для заданных конечных множеств переменных
1. Пусть x 2. Описать процедуру, которая перечисляет множество термов для заданных конечных множеств переменных, констант и функторов. 3. Пусть а) формула A теории L – не тавтология. б) в) L+ = L Доказать, что L+ противоречива, то есть, что ├ L+ B и ├ L+ ┐ B. 4. Доказать, что формула ( 5. Доказать методом резолюций: ├ L 6. Являются ли формулами следующие выражения: 7. Записать логическими формулами следующие сложные выска- зывания: а) «Этот человек студент или преподаватель». б) «Иванову нравится Ира или Маша». в) «Если при выполнении программы отклонение контролируемых параметров превысит допустимые нормы, то необходима корректировка программы или уточнение норм». г) «Если компьютер (ПК) при запуске не выдает ошибку при проверке оперативной памяти (ОП), то она исправна. Если при запуске он выдает ошибку при проверке ОП и память установлена правильно, то либо ОП дефектна, либо дефектна материнская плата. Тогда если эта ОП установлена правильно в контрольный ПК и он при запуске не выводит ошибки при проверке ОП, то ОП исправна». 8. К каким схемам относятся следующие рассуждения: а) «Если рабочий отсутствовал на работе, он не выполнил задание. Он не выполнил задание. Следовательно, он отсутствовал на работе». б) «Господин А живет постоянно в Киеве или Луганске. Он живет в Луганске, следовательно, он не живет в Киеве». Являются ли эти рассуждения логически правильными? 9. Записать логической формулой следующее изложение ТV сериала: «Если Марианна - не дочь дона Педро, то либо Хосе Игнасиас – отец Марианны, либо Луис Альберто – не ее брат. Если Луис Альберто – брат Марианны, то Марианна – дочь дона Педро и Хосе Игнасиас лжет. Если Хосе Игнасиас лжет, то либо Луис Альберто – не брат Марианны, либо Хосе Игнасиас – ее отец. Следовательно, Марианна – дочь дона Педро». 10. Доказать справедливость (истинность) умозаключения из примера 9, используя правило правильного рассуждения – закон противоречия (доказательство от противного). 11. К каким схемам рассуждений относятся следующие рассуждения: а) «Если студент отсутствовал на занятиях, он не выполнил задания. Он отсутствовал на занятиях. Следовательно, он не выполнил задания». б) «Мистер А женат на М или N. Он женат на М. Следовательно, он не женат на N». в) «Идет дождь или снег. Идет дождь. Следовательно, не идет снег». Являются ли данные рассуждения логическими правильными? 12. Записать формулой логики предикатов предложение, отражающее транзитивное свойство делимости целых чисел. 13. Записать предикатной формулой предложение, которое выражает для произвольных а,в,с Î N в модели М = (N, S, P, E), называемой в логике предикатов арифметикой натуральных чисел, где N – множество натуральных чисел, S, P, E – предикаты суммы, произведения и равенства соответственно: а) коммутативность умножения; б) ассоциативность сложения; в) дистрибутивность слева умножения относительно сложения; г) транзитивность равенства. 14. Пусть Q (х,у) – предикат порядка «х £ у». Рассмотреть различные варианты квантификации его переменных. Определить истинность получаемых выражений для различных случаев интерпретации области определения М предиката, х,у ÎМ. 15. Рассмотреть все возможные варианты навешивания кванторов на предикат D(х, у) – «х делится на у», определяемый на множестве натуральных чисел N. Дать словесные формулировки полученных высказываний и определить их истинность. 16. Какой смысл имеют предикатные формулы: а) " y " z $ x P(x,y,z); б) " x " y " z " u (P(x,y,z)&P(x,y,u) ® E(z,u)), где Р, Е – предикаты произведения и равенства, определенные на N. Истинны ли эти формулы? Привести примеры наборов переменных, иллюстрирующие заключение относительно истинности или ложности формул.
|

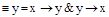 . Доказать, что формула L, содержащая только связку
. Доказать, что формула L, содержащая только связку  , является тавтологией тогда и только тогда, когда каждая переменная входит в нее четное количество раз.
, является тавтологией тогда и только тогда, когда каждая переменная входит в нее четное количество раз. - множество частных случаев A.
- множество частных случаев A.
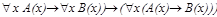 общезначима.
общезначима.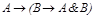 .
. 


