Интерпретация. Интерпретация I (прикладного) исчисления предикатов K с областью интерпретации (или носителем) М — это набор функций
Интерпретация I (прикладного) исчисления предикатов K с областью интерпретации (или носителем) М — это набор функций, которые сопоставляют: - каждой предметной константе а элемент носителя I(a), I(a) - каждому n - местному функтору f операцию I(f) на носителе, I(f): М n - каждому n - местному предикату Р отношение I(P) на носителе, I(P) Пусть х = (x 1 ,...) — набор (последовательность) переменных (входящих в формулу), a s = (s 1 ,...) — набор значений из М. Тогда всякий терм f(t 1 ,...,tn) имеет значение на s (из области М), то есть существует функция
Всякий атом P(t1,...,tn) имеет на s истинностное значение s*(P), определяемое следующим образом:
Если - формула - формула А - формула - формула Формула называется истинной в данной интерпретации I, если она выполнена на любом наборе s элементов М. Формула называется ложной в данной интерпретации I, если она не выполнена ни на одном наборе s элементов М. Интерпретация называется моделью множества формул Г, если все формулы из Г истинны в данной интерпретации. Всякая замкнутая формула истинна или ложна в данной интерпретации. Открытая (то есть не замкнутая) формула А(х, у, z,...) истинна в данной интерпретации тогда и только тогда, когда ее замыкание
|

 М;
М; М;
М;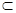 М n.
М n. : {t}
: {t}  А выполнена на s тогда и только тогда, когда формула А не выполнена на s;
А выполнена на s тогда и только тогда, когда формула А не выполнена на s; xi А выполнена на s тогда и только тогда, когда А выполнена на любом наборе s', отличающемся от s, возможно, только i -м компонентом.
xi А выполнена на s тогда и только тогда, когда А выполнена на любом наборе s', отличающемся от s, возможно, только i -м компонентом. xi А выполнена на s тогда и только тогда, когда А выполнена на каком-либо наборе s', отличающемся от s, возможно, только i -м компонентом.
xi А выполнена на s тогда и только тогда, когда А выполнена на каком-либо наборе s', отличающемся от s, возможно, только i -м компонентом.


