Выводимость
Пусть F1,..., Fn, G — формулы теории T, то есть F1,..., Fn, G
где формулы F1,..., Fn называются посылками, а формула G — заключением. Обозначение правила вывода справа от черты, разделяющей посылки и заключение, часто опускают, если оно ясно из контекста. Выводом формулы G из формул F1,..., Fn в формальной теории T называется такая последовательность формул E1,...,Ek, что Еk = G, а любая формула Еi (i < k) является либо аксиомой (Ei
где формулы F1,..., Fn называются гипотезами вывода. Если теория T подразумевается, то ее обозначение обычно опускают. Приведем простейшие правила выводимости. Если ├ T G, то формула G называется теоремой теории T (то есть теорема — это формула, выводимая только из аксиом, без гипотез). Если Г ├ T G, то Г, Г, А ├ T А. Действительно, вывод формулы А из системы гипотез Г, А состоит из одной формулы. Если Г, А, В ├ T G, то Г, В,А ├ T G. Если Г ├ T А, Г ├ T В и А, В ├ T С, то Г ├ T С. Действительно, пусть А 1,…,Аn – вывод формулы А из Г; В 1,…,Вm – вывод формулы В из Г, С 1,…,Сk - вывод формулы С из А, В. Тогда очевидно, что А 1,…,Аn, В 1,…,Вm, С 1,…,Сk есть вывод формулы С из Г. Если Г, А ├ T В и Г ├ T А, то Г ├ T В (правило удаления выводимой гипотезы). Пусть В 1,…,Вn – вывод формулы В из Г, А. Если в этом выводе не встречается формула А, то имеем вывод В из Г, если в этом выводе встречается формула А, то пусть В i1,…,Вik – все вхождения формулы А в вывод. Пусть также А 1,…,Аm – вывод А из Г. Тогда B1,…,Вi1-1,А 1,…,Аm,Bi1+1,…,Bi2-1,А 1,…,Аm, Bi2+1,…,Bik-1,А 1,…,Аm,Bik+1,…,Bm - вывод формулы В из Г. При изучении формальных теорий нужно различать теоремы формальной теории и теоремы о формальной теории или метатеоремы. Это различие не всегда явно формализуется, но всегда является существенным. В этой главе теоремы конкретной формальной теории, как правило, записываются в виде формул, составленных из специальных знаков, а мета теоремы формулируются на естественном языке, чтобы их легче было отличать от теорем самой формальной теории.
|

 F. Если существует такое правило вывода R, R
F. Если существует такое правило вывода R, R 
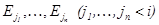 . Если в теории T существует вывод формулы G из формул F1,..., Fn, то это записывают следующим образом:
. Если в теории T существует вывод формулы G из формул F1,..., Fn, то это записывают следующим образом: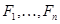 ├ T G,
├ T G, ├ T G, где Г и
├ T G, где Г и 


