Пример 4.3.
А Теорема 4.1. Пусть А — некоторая формула. Тогда: 1. Если А — тавтология, то ┐А — противоречие, и наоборот; 2. Если А — противоречие, то ┐A — тавтология, и наоборот; 3. Если А — тавтология, то неверно, что А — противоречие, но не наоборот; 4. Если А — противоречие, то неверно, что А — тавтология, но не наоборот. Доказательство. Очевидно из определений. Теорема 4.2. Если формулы А и А → В — тавтологии, то формула В — тавтология. Доказательство. От противного. Пусть 1(В) = Л. Но 1(А) = И, так как А — тавтология, значит, 1(А → В) = Л, что противоречит предположению о том, что А → В — тавтология. Можно перечислить наиболее важные тавтологии (А, В, С – произвольные формулы): 1) А®А; 2) А®(В®А); 3) (А®В)®((В®С)®(А®С)) (цепное рассуждение); 4) (А®(В®С))®((А®В)®(А®С)); 5) (А&В)®А, (А&В)®В; (4.1) 6) А®(В®(А&В)); 7) А®(АÚВ), В®(АÚВ); 8) (┐В ®┐А)®((┐В®А)®В); 9) ((А ®В)®А)®А (закон Пирса). Немаловажную роль играют логическое следование и логическая эквивалентность формул. Говорят, что формула В логически следует из формулы А (обозначается А Теорема 4.3. (Р® Q)Û(┐РÚQ). Доказательство. Для доказательства достаточно проверить, что формулы действительно имеют одинаковые истинностные значения при всех интерпретациях.
Теорема 4.4. Если А, В, С — любые формулы, то имеют место следующие логические эквивалентности: 1. A 2. А 3. А 4. A 5. (A&B) 6. A 7. A 8. ┐ (┐ A) = A; ┐ (A Ú B) = ┐ A&┐ B; 9. ┐ (A&B) = ┐ A 10. A Доказательство всех эквивалентностей (они нам уже знакомы по разделу 3) непосредственно проводится построением таблиц истинности. Анализируя все полученные результаты, можем, таким образом, заметить, что алгебра Теорема 4.5. P1 &... & Pn Доказательство. Необходимость. Пусть I(P1 &... & Pn) = И. Тогда I(Q) = И и I(P1 &... & Pn Пусть I(P1 &... & Pn) = Л. Тогда I(P1 &... & Pn Достаточность. Пусть I(P1 &... & Pn) = И. Тогда I(Q) = И, иначе бы формула P1 &... & Pn Теорема 4.6. P1 &... & Pn Доказательство. По предыдущей теореме P1 &... & Pn ┐ (P1 &... & Pn = ┐┐(P1 &... & Pn) & ┐Q)=P1 &... & Pn & ┐Q. Определим преобразование логических фигур с помощью подстановки. Пусть А — некоторая формула, в которую входит переменная х (обозначается А (... х...)) или некоторая подформула В (обозначается A (… В...)), и пусть С — некоторая формула. Тогда А (...х...){ С / / х } обозначает формулу, полученную из формулы А подстановкой формулы С вместо всех вхождений переменной х, а А (... B...){ С / B } обозначает формулу, полученную из формулы А подстановкой формулы С вместо некоторых (в частности, вместо одного) вхождений подформулы В. Теорема 4.7. Если А(... х...) — тавтология и В — любая формула, то А(...х...){В//х} — тавтология. Доказательство. Пусть С = A (... х...){В // х}. Пусть I — интерпретация С (она не содержит x). Пусть Теорема 4.8. Если А (... В...) и В = С, a D = А (... В...){ С/В }, то А=D. Доказательство. Пусть I — любая интерпретация. Тогда I (В) = I (С), значит I (A) = I (D).
|

 ┐A — тавтология, А & ┐ А — противоречие, А → ┐ А — выполнимая формула, она истинна при А = Л.
┐A — тавтология, А & ┐ А — противоречие, А → ┐ А — выполнимая формула, она истинна при А = Л. В), если формула В имеет значение И при всех интерпретациях, при которых формула А имеет значение И. Говорят, что формулы А и В логически эквивалентны (обозначается А
В), если формула В имеет значение И при всех интерпретациях, при которых формула А имеет значение И. Говорят, что формулы А и В логически эквивалентны (обозначается А  В,
В,  или просто А = В), если они являются логическим следствием друг друга. Логически эквивалентные формулы имеют одинаковые значения при любой интерпретации.
или просто А = В), если они являются логическим следствием друг друга. Логически эквивалентные формулы имеют одинаковые значения при любой интерпретации. {И,JI};
{И,JI};  является булевой алгеброй, которая называется алгеброй высказываний.
является булевой алгеброй, которая называется алгеброй высказываний. Q тавтология.
Q тавтология. . Тогда
. Тогда  , но
, но 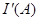 = И, следовательно I(C) = И.
= И, следовательно I(C) = И.


