Определения. Корректность этих умозаключений основана на внутренней структуре самих предложений и на смысле слов «всякий» и «существует».
Логика высказываний – очень узкая логическая система. Есть такие типы логических рассуждений, которые не могут быть осуществлены в рамках логики высказываний, например:
Корректность этих умозаключений основана на внутренней структуре самих предложений и на смысле слов «всякий» и «существует». Рассмотрим предложения, зависящие от параметров, например: «х – четное число», «х меньше y», «x + y = z», «u и v – братья». Если в первых трех предложениях заменить x, y и z некоторыми числами, а в последнем подставить имена членов некоторой семьи, то полученные высказывания могут быть истинными или ложными. Например, для х =5, y =2, z =7, u – Петр, v – Иван получим: «5 – четное число», «5 меньше 2», «5+2=7», «Петр и Иван – братья». Предложения такого типа называются предикатами. Точнее, предикатом P(x1,…,xn) называется функция, переменные которой принимают значения из некоторого множества М, а сама она принимает два значения: истинное (И) и ложное (Л), т.е. P(x1,…,xn):М Предикат от n аргументов называют n-местным предикатом и обозначают полностью P(n)(x1,…,xn), если нужно подчеркнуть число аргументов. Высказывания считают нуль-местными предикатами. Над предикатами можно производить обычные логические операции. В результате получаются новые предикаты Например: 1. Пусть P(1)(x) означает предикат «х делится на 2», а Q(1)(х) – предикат «х делится на 3». Тогда выражение P(1)(x) &Q(1)(х) означает предикат «х делится на 2 и х делится на 3», т.е. определяет предикат делимости на 6. 2. Пусть S(2)(х,у) означает предикат «х=у». Он принимает значение И тогда и только тогда, когда х=у. В этом случае выражение ┐ S(2)(х,х) ÞS(2)(х,у) определяет предикат, принимающий значение И при любых х и у. Кроме операций логики высказываний будем применять еще операции связывания квантором. Квантор всеобщности. Пусть Р(х) – предикат, принимающий значение И или Л для каждого х ÎМ. Тогда под выражением " хР(х) будем подразумевать высказывание истинное, когда Р(х) истинно для каждого элемента х из М, и ложное – в противном случае. Символ " х называется квантором всеобщности и запись " хР(х) читается так: «для всех х Р(х)». Это высказывание уже не зависит от х. Квантор существования. Пусть Р(х) – предикат. Под выражением $ х Р(х) будем понимать высказывание истинное, если существует элемент множества М, для которого Р(х) истинно, и ложное – в противном случае. Символ $ х называется квантором существования и запись $ хР(х) читается так: «существует х, такое, что (или для которого) Р(х)». Для предикатов, рассмотренных чуть ранее, можем записать:
Введем теперь строгие определения для исчисления предикатов. (Чистое) исчисление предикатов (первого порядка) — это формальная теория К, в которой определены следующие компоненты. 1. Алфавит: связки основные ┐, дополнительные &, служебные символы (,) Î (, ’, ’,) кванторы всеобщности существования предметные константы переменные предметные предикаты P, Q,... функторы f, q,... С каждым предикатом и функтором связано некоторое натуральное число, которое называется арностью, или иногда местностью. 2. Формулы имеют следующий синтаксис:
| ┐;
При этом должны быть выполнены следующие контекстные условия: в терме f (t 1 ,...,tn) функтор f должен быть n - местным. В атоме (или атомарной формуле) P(t 1 ,...,tn) предикат Р должен быть n - местным. Вхождения переменных в атомарную формулу называются свободными. Свободные вхождения переменных в формулах А и В остаются свободными в формулах Например, рассмотрим формулу Язык теории L не содержит кванторов, поэтому понятия свободного и связанного вхождения переменных не применимы непосредственно. Обычно для удобства полагают, что все формулы теории L замкнуты. Формулы вида А и ┐ А, где А — атом, называются литеральными формулами (или литералами). В формулах Обычно связки и кванторы упорядочивают по приоритету следующим образом: ┐, Например: а) терм у свободен для переменной х в формуле Р(x), но тот же терм у не свободен для переменной х в формуле б) терм f(x, z) свободен для переменной х в формуле
Переход от предиката Р(х) к " х Р(х) или $ х Р(х) называется связыванием переменной х, или навешиванием квантора на переменную х, или квантификацией переменной х. Выражение " х Р(х) и $ х Р(х) не зависят от х и при фиксированных Р и предметного множества М имеет вполне определенные значения, представляя вполне конкретные высказывания относительно всех х в предметной области М. Возвращаясь к определению предиката можно отметить, что высказывание есть просто нуль местный предикат. Навешивая кванторы на многоместные предикаты и вообще на любые логические выражения, мы тем самым и определяем область действия квантора $ х или " х и все вхождения х в эти выражения являются связными. Рассмотрим решение некоторых примеров.
Пример 4.4. Пусть N (х) – предикат «х – натуральное число». Рассмотреть варианты навешивания кванторов, интерпретировать и определить их истинность. Решение. " х N(х) –«все числа натуральные». Это высказывание истинно на любом множестве натуральных чисел и ложно, если М содержит хоть одно ненатуральное число (например, целое отрицательное).
Пример 4.5. Пусть предикат Р(х,у) описывает отношение «х любит у» на множестве людей. Проанализировать варианты навешивания кванторов и дать интерпретацию. Решение. Используя взаимно однозначное соответствие между отношениями предикатами, можно проиллюстрировать решение схемами (рис. 4.1.).
Рис. 4.1. Иллюстрация влияния кванторов
Интерпретация: " х $ y Р(х,у) – «для любого х существует у, которого он любит». $ у " х Р(х,у) – «существует такой у, которого любят все х». " х " уР(х,у) - «все х любят всех у». $ х $ у Р(х,у) – «найдется х, который любит кого-то из у» или «найдется человек, который кого-то любит». $ х " у Р(х,у) – «существует х, который любит всех у». " у $ х Р(х,у) – «для любого из у найдется х, который его любит».
Аксиомы (логические): любая система аксиом исчисления высказываний, плюс P 1: P 2: A(t) где терм t свободен для переменной х в формуле А.
Правила вывода:
где формула А содержит свободные вхождения переменной х, а формула В их не содержит. Исчисление предикатов, которое не содержит предметных констант, функторов, предикатов и собственных аксиом, называется чистым. Исчисление предикатов, которое содержит предметные константы и/или функторы и/или предикаты и связывающие их собственные аксиомы, называется прикладным. Исчисление предикатов, в котором кванторы могут связывать только предметные переменные, но не могут связывать функторы или предикаты, называется исчислением первого порядка. Исчисления, в которых кванторы могут связывать не только предметные переменные, но и функторы, предикаты или иные множества объектов, называются исчисленьями высших порядков. Практика показывает, что прикладного исчисления предикатов первого порядка оказывается достаточно для формализации содержательных теорий во всех разумных случаях.
Соответствие между предикатами, отношениями и функциями
n – местный предикат можно рассматривать как функцию Р (х 1,… х n) от n переменных хi Î Мi, где Мi - предметные области, а РÎВ={0,1}={И,Л}. Таким образом, предикат Р (х 1,… х n) является функцией типа Р: М1 ´М2 ´… ´Мn ®В, или, если предметная область едина для всех переменных, то имеем Р: Мn ®В. Из рассмотренного очевидно, что для любых М и n существует однозначное соответствие между n-местными отношениями R ÍМn и предикатами Р (х 1,… х n), Мn ®В: - каждому n – местному отношению R соответствует предикат Р (х 1,… х n) такой, что Р (а 1,… а n)=1, если и только если (а 1,… а n)ÎR; - всякий предикат Р (х1,…х n) определяет отношение R такое, что (а 1,… а n)Î R, если и только если Р (а 1,… а n)=1. При этом R задает область истинности предиката P. Рассмотрим теперь функцию f (х 1,…, х n), f: Мn®M. Тогда можно видеть, что всякой функции f: Мn ®M соответствует предикат Р (х 1,… х n+1), Р: Мn+1 ®В, такой что Р(а1,…аn+1)=1, если и только если f (а 1,… а n)= а n+1. Понятие предиката шире понятия функции (см. рис. 4.1.), поэтому обратное соответствие (от (n+1)-местного предиката к n–местной функции) возможно не всегда, а только для таких предикатов, для которых выполняется условие, связанное с однозначностью функции: Р(а1,…аn+1)=0 ® ("а¢n+1ÎМ|а¢n+1¹аn+1 Р(а1,…а¢n+1)=0. (4.3.) Аналогичное соответствие имеется между подмножеством отношений {R¢}Ì{R} и множеством функций {f}. Для этого класса отношений выполняется условие (а 1,… а n+1)ÎR¢ ® (" а¢;n+1ÎМ| а¢;n+1¹ а n+1 (а 1,… а¢;n+1)ÎR¢). (4.4.) Пример 4.6. Каким отношениям и функциям соответствуют предикаты, определенные на множестве натуральных чисел? 1. Предикат суммы S: N 3 ®В: S(х1,х2,х3)=1 тогда и только тогда, когда х 1+ х 2= х 3. 2. Предикат порядка Q:N 2®В: Q (х 1, х 2)=1 тогда и только тогда, когда х 1£ х 2.
|

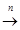 {И,Л}.
{И,Л}.

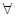



 формула
формула  =
= 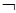 А и А
А и А 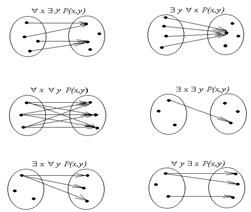
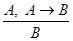 Modus ponens,
Modus ponens, 



