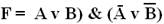Таблицы истинности

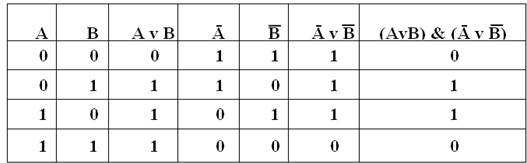
Таблицы, в которых логические операции отражают результаты вычислений сложных высказываний при различных значениях исходных простых высказываний, называются таблицами истинности.

Простые высказывания обозначаются переменными (например, A и B).

При построении таблиц истинности целесообразно руководствоваться определённой последовательностью действий:

1) необходимо определить количество строк в таблице истинности. Оно равно количеству возможных комбинаций значений логических переменных, входящих в логическое выражение. Если количество логических переменных равно п, то:

количество строк = 2ⁿ.

В нашем случае логическая функция

имеет 2 переменные и, следовательно, количество строк в таблице истинности должно быть равно 4;

2) необходимо определить количество столбцов в таблице истинности, которое равно количеству логических переменных плюс количество логических операций.

В нашем случае количество переменных равно двум: А и В, а количество логических операций — пяти (таблица 8), то есть количество столбцов таблицы истинности равно семи;

3) необходимо построить таблицу истинности с указанным количеством строк и столбцов, обозначить столбцы и внести в таблицу возможные наборы значений исходных логических переменных;

4) необходимо заполнить таблицу истинности по столбцам, выполняя базовые логические операции в необходимой последовательности и в соответствии с их таблицами истинности.

Теперь мы можем определить значение логической функции для любого набора значений логических переменных.

Таблица 8 – Таблица истинности логической функции