Стоячие волны.
Особый интерес представляет собой результат интерференции двух волн с одинаковой амплитудой и частотой, распространяющихся навстречу друг другу. На опыте это можно осуществить, если на пути бегущей волны перпендикулярно к направлению распространения поставить хорошо отражающую преграду. В результате сложения (интерференции) падающей и отраженной волн возникнет так называемая стоячая волна. Пусть падающая волна описывается уравнением (16), а отраженная – уравнением (17). Сложениеэтих двух волн дает Y = y1 + y2:
Y = 2A cosωt cos
Это уравнение, называемое уравнением стоячей волны, удобно в дальнейшем анализировать в виде:
Y = 2A cosωt, (27)
где множитель
A0 =
является амплитудой стоячей волны. Как видноиз выражения (28), амплитуда стоячей волны зависит от координаты точки, но не зависит от времени. У бегущей плоской волны амплитуда не зависит ни от координаты, ни от времени (при отсутствии затухания). Примечание 4 Проделаем необходимые преобразования для определения суммарной волны. Y = A[sin ω(t – x/v) + sin ω(t + x/v)] = = 2Acos[ω/2(t – x/v – t - x/v)] sin[ω/2(t – x/v + t + x/v)] = 2Acos(-ωx/v) sin ωt = = 2Acos(ωx/v) sin ωt. Или Y = A0sin ωt, где A0 = 2Acos(ωx/v).
Множитель sin ωt показывает, что в точках среды возникает колебание с той же частотой, что и колебания встречных волн. Так как функция Точки стоячей волны, в которых амплитуда колебаний равна нулю, называют узлами, а точки, в которых она максимальна, называют пучностями. Координаты пучностей стоячей волны можно определитьизравенства или
тогда где k = 0, 1, 2,.... Координаты узлов определяютсяиз равенства
Или откуда следует x= Из выражений (29) и (30) следует, что расстояние между соседними узлами (или между соседними пучностями) равно
Рис. 3
При отражении волн на границе двух сред возникает либо узел, либо пучность (в зависимости от так называемых акустических сопротивлений сред). Акустическим сопротивлением среды называют величину В отличие от бегущей волны, которая переносит энергию, в стоячей волне переноса энергии нет. Бегущая волна может двигаться вправо или влево, а у стоячей волны нет направления распространения. Под термином "стоячая волна" нужно понимать особое колебательное состояние среды, образованное интерферирующими волнами. В момент, когда частицы среды проходят положение равновесия, полная энергия частиц, захваченных колебанием, равна кинетической. Она сосредоточена в окрестностях пучностей. Напротив, в момент, когда отклонение частиц от положения равновесия максимально, их полная энергия является уже потенциальной. Она сосредоточена вблизи узлов. Таким образом, два раза за период происходит переход энергии от пучностей к соседним узлам и наоборот. В результате средний по времени поток энергии в любом сечении стоячей волны равен нулю. Стоячие волны различной природы (упругие, электромагнитные) проявляются во многих физических явлениях (например, колебания струн музыкальных инструментов, камертонов, колебания электрического тока в вибраторах антенн, голография). Если плоская звуковая волна распространяется вдоль оси цилиндра в столбе воздуха, ограниченном его стенками и поршнем (рисунок 4), то в результате сложения падающей и отраженной от поршня волн образуется стоячая волна. Вследствие разности акустических сопротивлений поршня и воздуха на границе с поршнем будет находиться узел стоячей волны. На открытом же конце цилиндра будет находиться пучность.
Рис. 4 В этом случае в цилиндре могут установиться лишь такие стоячие колебания, при которых на длине столба L укладывается нечетное число четвертей длин волн, т.е. выполняется условие:
где n - любое целое число (n ≠ 0). Из этого условия можно выразить длину волны
или частоту колебаний
Возникающие колебания частотами, удовлетворяющими условию (33), называются собственными колебаниями системы. Колебания с наименьшей частотой Если частота фиксирована, то устойчивых колебаний можно добиться, изменяя L путем перемещения поршня и добиваясь таким образом выполнения условия (30). Расстояние между двумя соседними положениями поршня, при которых возникают устойчивые колебания, равно
|

 (26)
(26) (28)
(28) - может принимать значения от 0 до 1, то амплитуда стоячей волны в зависимости от координаты точки может принимать значения (А0): от 0 до 2.
- может принимать значения от 0 до 1, то амплитуда стоячей волны в зависимости от координаты точки может принимать значения (А0): от 0 до 2.
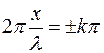
 (29)
(29)
 ,
, (30)
(30)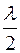 , а расстояние между ближайшими узлом и пучностью равно
, а расстояние между ближайшими узлом и пучностью равно 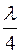 (рисунок- 3). Уравнение (27) показывает, что все точки среды, расположенные между двумя соседними узлами, колеблются в одной фазе, причем значение фазы определяется только временем. Для бегущей волны как следует из (16), фаза определяется как временем, так и пространственной координатой. В этом еще одно отличие между данными волнами. При переходе через узел фаза стоячей волны скачкообразно изменяется на 180о. Кривые 1 и 5, приведенные на рисунок 3, соответствуют максимальному отклонению частиц от положения равновесия в моменты времени, отличающиеся на половину периода. В другие моменты времени кривая отклонения частиц будет располагаться между этими двумя.
(рисунок- 3). Уравнение (27) показывает, что все точки среды, расположенные между двумя соседними узлами, колеблются в одной фазе, причем значение фазы определяется только временем. Для бегущей волны как следует из (16), фаза определяется как временем, так и пространственной координатой. В этом еще одно отличие между данными волнами. При переходе через узел фаза стоячей волны скачкообразно изменяется на 180о. Кривые 1 и 5, приведенные на рисунок 3, соответствуют максимальному отклонению частиц от положения равновесия в моменты времени, отличающиеся на половину периода. В другие моменты времени кривая отклонения частиц будет располагаться между этими двумя.
 . Если среда, от которой отражается волна, обладает более высоким акустическим сопротивлением, чем та, в которой эта волна возбуждается, то на границе раздела образуется узел. В этом случае фаза волны при отражении меняется на противоположную (на 180°). При отражении волны от среды с меньшим акустическим сопротивлением изменение фазы колебаний не происходит.
. Если среда, от которой отражается волна, обладает более высоким акустическим сопротивлением, чем та, в которой эта волна возбуждается, то на границе раздела образуется узел. В этом случае фаза волны при отражении меняется на противоположную (на 180°). При отражении волны от среды с меньшим акустическим сопротивлением изменение фазы колебаний не происходит.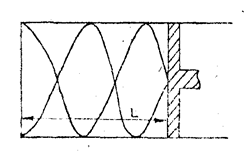
 (31)
(31) (32)
(32) (33)
(33) называют основным тоном, а остальные, с частотами 3
называют основным тоном, а остальные, с частотами 3  o, 5
o, 5 


