Лабораторная работа №4
Исследование реактивных электрических фильтров.
ВВЕДЕНИЕ ОСНОВНЫЕ СВДЕНИЯ ИЗ ТЕОРИИ ФИЛЬТРОВ Электрическим фильтром называется четырехполюсник, предназначенный для пропускания сигналов одних частот и подавления (задержки) сигналов других частот. Для оценки частотных свойств фильтра используется понятие полосы пропускания. Полосой пропускания фильтра называется интервал частот, на котором величина собственного затухания фильтра не превышает заданного уровня. Фильтры классифицируются по следующим признакам: 1.По пропускаемым частотам: - фильтры низких частот (низкочастотные) пропускают сигналы, начиная с нулевой частоты и до некоторой граничной частоты; - фильтры высокой частоты (высокочастотные) пропускают сигналы, начиная с некоторой граничной частоты до сколь угодно большого их значения; - фильтры полосовые пропускают сигналы, лежащие в определенной полосе частот, ограниченной нижним и верхним значениями; - режекторные фильтры не пропускают сигналы только в определенной полосе частот и по частотным свойствам являются противоположностью полосовым фильтрам. 2. По схемам простейших звеньев: - Г-образные; - Т-образные; - П-образные. 3. По числу простейших звеньев, используемых в фильтре: - однозвенные; - многозвенные (двухзвенные, трехзвенные и т. д.). 4. По виду характеристик: - фильтры типа – k; - фильтры типа – m. 5. По типам элементов схемы. 5.1. Пассивные фильтры - без усилительных элементов: - реактивные (из L - С элементов); - безиндуктивные (из R - C элементов); - пьезоэлектрические. 5.2. Активные фильтры: - фильтры, выполненные с применением транзисторов; - фильтры, выполненные с применением электронных ламп.
Электрический фильтр представляет собой четырёхполюсник, поэтому при анализе фильтров широко используется теория четырёхполюсников. В данной лабораторной работе изучаются реактивные фильтры, поэтому элементами этих фильтров являются катушки индуктивности и конденсаторы. Электрическая схема будет обладать свойствами фильтра, если в ней находятся и катушка индуктивности и конденсатор. Схема, состоящая только из катушек индуктивности или только из конденсаторов, не может обладать свойствами фильтра. В зависимости от расположения названных элементов в схеме одна и та же по конструкции схема (на пример Г – образная) будет обладать свойствами низкочастотного или высокочастотного фильтра. При общем рассмотрении теории фильтров удобно элементы, из которых состоят фильтры, обозначать через Z 1 и Z 2. Элементы фильтров, как было сказано, являются комплексными величинами, однако точки над этими обозначениями принято не ставить. Простейшая схема фильтра состоит из двух элементов, соединённых по Г - образной схеме (рис.1).
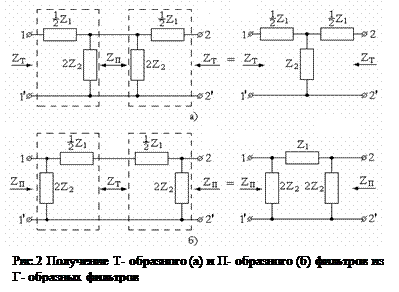
Как видно из рисунка, возможны два варианта соединения элементов. Это приводит только к изменению входных и выходных сопротивлений фильтров. Через Z Т и Z П обозначаются входные и выходные характеристические сопротивления фильтров. Более сложным схемным решением фильтров являются Т – образные и П – образные фильтры (рис. 2). Эти фильтры получены путём каскадного соединения Г – образных фильтров, меняя последовательность их соединения.
Фильтром называется устройство, пропускающее сигналы одних частот и подавляющее сигналы других частот. Фильтры называются тем видом частот, которые они пропускают. Так, фильтры, пропускающие низкие частоты, называются низкочастотными и т.д. Фильтр представляет собой четырехполюсник (рис.4.1).
Рис.4.1. Условное обозначение фильтра в виде четырехполюсника
Для оценки степени пропускания или подавления частотно-изменяющегося сигнала используется понятие собственного подавления фильтра по напряжению:
где - - размерность затухания измеряется в Неперах (Нп). Для экспериментального исследования частотных свойств фильтра на вход его подается сигнал с заданной частотой и с напряжением U1 на выходе измеряется напряжение U2. Беря отношение этих величин, находят К(ω) для заданной частоты и по формуле 1 определяют величину подавления. Задавая различные частоты входного сигнала, строится зависимость В лабораторной работе исследуются низкочастотные фильтры, показанные на рисунке 4.2 и высокочастотные фильтры, показанные на рисунке 4.3. Низкочастотные фильтры
Рис.4.2. Схемы Г-образного (а) и Т-образного (б) низкочастотных фильтров
При расчетном анализе низкочастотных фильтров собственное подавление для Г – образного и Т - образного фильтров определяется по следующим формулам.
Г– образный низкочастотный фильтр
Здесь через
Частота среза для всех видов фильтров характеризуется тем, что она лежит на границе между интервалом частот, где осуществляется их пропускание и интервалом частот, где осуществляется их подавление. Элементы схемы Г – образного низкочастотного фильтра имеют следующие значения:
Примечание: При величине
Т – образный низкочастотный фильтр
Через
Элементы схемы Т – образного низкочастотного фильтра имеют следующие значения:
Примечание: При величине
Высокочастотные фильтры
Рис.4.3. Схемы Г-образного (а) и Т-образного (б) высокочастотных фильтров
При расчетном анализе высокочастотных фильтров их собственное подавление определяется по формулам: Г – образный высокочастотный фильтр
Здесь через
Здесь: L=2 мГн; С=10000 пФ. Примечание: При величине Т – образный высокочастотный фильтр
Здесь через
Здесь: L=1 мГн; С=10000 пФ. Примечание: При величине 2. ПРЕДВАРИТЕЛЬНАЯ ПОДГОТОВКА К ВЫПОЛНЕНИЮ ЛАБОРАТОРНОЙ РАБОТЫ В лабораторной работе используются индуктивности стенда, на котором исследовались частотные характеристики резонансных контуров. Величина емкости конденсатора для всех бригад принимается равной При подготовке к лабораторной работе рассчитать и построить графики затухания вкоординатах а=φ(ω), для всех четырех схем фильтров, приведенных на рисунок 4.2 и рисунок 4.3. Для Г-образного и Т-образного фильтров нижних частот результаты расчетов свести в таблицу 4.1.
Таблица 4.1.
То же проделать для Г-образного и Т-образного фильтров верхних частот. Результаты расчетов свести в таблицу 4.2.
Таблица 4.2.
3. ВЫПОЛНЕНИЕ РАБОТЫ В качестве источника синусоидального напряжения используется генератор с диапазоном частот от 20 Гц до 200 кГц. Напряжение на входе и на выходе схемы фильтра измеряется с помощью электронных вольтметров. Для снятия частотных характеристик входное напряжение поддерживать постоянным. Схема для снятия частотных характеристик фильтров показана на рис.4.4. Величину RН можно взять 400÷500 Ом.
Рис.4.4. Схема установки для снятия частотных характеристик фильтров.
Результаты экспериментов свести в таблицу 4.3для фильтров нижних частот и в таблицу 4.4для фильтров верхних частот соответственно.
Таблица 4.3.
Таблица 4.4.
Экспериментальные графики зависимости aэ=φ(ω) нанести на расчетные графики зависимости а=φ(ω).
4. СОДЕРЖАНИЕ ОТЧЕТА В отчете должно быть отражено следующее: 1. Результаты домашней подготовки: расчеты, графики, таблицы в соответствии с разделом 2 описания лабораторной работы. Графики должны быть выполнены на миллиметровой бумаге. 2.Таблицы и графики результатов эксперимента. Экспериментальные графики должны быть совмещены с расчетными. 3. Мотивированное объяснение расхождения результатов расчета и эксперимента.
5. КОНТРОЛЬНЫЕ ВОПРОСЫ 1. Дать понятие фильтра определенных частот. 2. Объяснить физически характер частотной зависимости для фильтров нижних и верхних частот. 3.Объяснить увеличение крутизны графика а=φ(ω) при переходе от Г-образных фильтров к Т-образным.
ЛИТЕРАТУРА: 1. Г.И.Атабеков «Основы теории цепей» Изд. «Энергия» г. Москва 1969г 2. В.Н.Станевко «Основы теории цепей» Часть 1, г. Рыбинск, 2009г. 3. В.Н.Станевко «Основы теории цепей» Часть 2, г. Рыбинск, 2013г.
Оглавление Лабораторная работа №1. ………..……..3 Лабораторная работа №2. 7 Лабораторная работа №3. 14 Лабораторная работа №4. 24 ЛИТЕРАТУРА.. 30
|



 (Нп), (1)
(Нп), (1)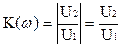 - модуль комплексного коэффициента передачи четырехполюсника (фильтра),
- модуль комплексного коэффициента передачи четырехполюсника (фильтра), .
.

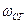 обозначается частота среза для Г – образного фильтра, которая определяется по формуле:
обозначается частота среза для Г – образного фильтра, которая определяется по формуле: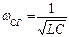
 мГн, С=10000 пФ.
мГн, С=10000 пФ.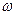 меньше величины
меньше величины  принимается равной нулю. Это объясняется тем, что формула для подавления хорошо аппроксимирует функцию
принимается равной нулю. Это объясняется тем, что формула для подавления хорошо аппроксимирует функцию  только в области подавления и не соответствует области пропускания.
только в области подавления и не соответствует области пропускания.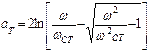
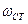 обозначается частота среза для Т – образного низкочастотного фильтра, которая определяется по формуле:
обозначается частота среза для Т – образного низкочастотного фильтра, которая определяется по формуле: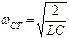
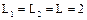 мГн, С=20000 пФ.
мГн, С=20000 пФ.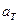 принимается равной нулю.
принимается равной нулю.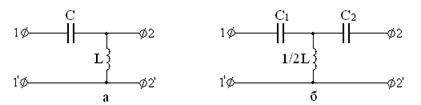
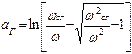
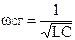

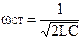 .
.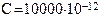 Ф.
Ф.



