Закон сохранения импульса.
1. Совокупность тел, частиц (например, в газе) или отдельное твердое можно рассматривать как систему материальных точек. Если система с течением времени изменяется, то это означает, что изменяется ее состояние. Зная законы действующих на частицы системы сил и состояние системы в начальный момент времени, можно с помощью уравнений движения рассчитать состояние системы в любой момент времени. Но в некоторых случаях это может быть задачей достаточно сложной (сложна сама система или неизвестны законы действующих сил, или детальное рассмотрение поведения отдельных частиц системы не имеет смысла, например, в газе). Возникает вопрос: нет ли каких-либо общих принципов, которые позволили бы иначе подойти к решению задач и обойти возникшие трудности? Оказалось, такие принципы есть. Это законы сохранения энергии, импульса и момента импульса (см. [7], стр. 52-57). Эти законы справедливы не только в рамках классической механики. Все они являются универсальными законами природы, выполняются и в макромире, и в микромире, и во всей Вселенной. В настоящее время неизвестно ни одного эксперимента и ни одного физического явления, в котором упомянутые универсальные законы сохранения нарушались бы. Закон сохранения импульса выполняется для замкнутых систем (см. § 2.2.1 п.1). 2.Справедливость закона сохранения импульса можно показать для замкнутой системы, состоящей из двух тел, применяя второй и третий законы Ньютона. Пусть первое тело, имеющее массу m 1, движется со скоростью При столкновении тела взаимодействуют друг с другом, и, согласно Третьему закону Ньютона, сила Рассматриваемая нами замкнутая система состояла из двух тел, полный вектор импульса этой системы
Если система состоит из N тел, то P = m1 ∙v 1 + m2 ∙v 2 +........+ mN ∙v N есть полный вектор импульса замкнутой системы, и P = const. Закон сохранения импульса (ЗСИ). Полный вектор импульса замкнутой системы есть величина постоянная при любых взаимодействиях внутри данной системы. Только внешние силы изменяют импульс системы. 3. Если векторная сумма внешних сил не равна нулю, то надо посмотреть, нет ли такого направления, вдоль которого внешние силы не действуют или сумма их проекций на это направление равна нулю. Если такое направление в движении тел, входящих в систему, есть, то можно применять закон сохранения для проекции полного вектора импульса системы на выделенное направление.
|

 ,второе тело, масса которого m 2 , движется со скоростью
,второе тело, масса которого m 2 , движется со скоростью  2.
2. 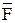 12 =-
12 =-  изменит импульс первого тела, можно записать
изменит импульс первого тела, можно записать  , точно так же можно записать, что сила F 21 изменит импульс второго тела:
, точно так же можно записать, что сила F 21 изменит импульс второго тела:  . Подставим значения F 12 и F 21 в третий закон Ньютона:
. Подставим значения F 12 и F 21 в третий закон Ньютона:  - одно и то же, то:
- одно и то же, то:  =-
=-  или
или  =
=  .
.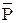 =
=  +
+  ,
, +
+ 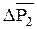 =
= 


