Общая постановка задачи. Линейная модель
В практике финансово-экономического анализа довольно часто возникает необходимость определить барьерное (критическое, предельно допустимое) значение некоторого параметра. Под барьерным значением параметра понимается такая его величина, превышение которой приводит к положительному или отрицательному конечному экономическому результату в рамках некой производственной или финансовой системы. Например, если речь идет об определении объема производства какого-то продукта, то критическим его значением является такой объем выпуска, при котором полученная прибыль равна нулю. Превышение этого объема дает прибыль, производство в меньшем объеме оказывается убыточным. Подобная и многие другие, сходные по общей постановке задачи решаются с помощью метода барьерной (критической) точки (break-even analysis). Этот метод широко используется в финансовом проектировании, при разработке бизнес-планов и при решении ряда финансовых проблем. Наиболее простая постановка задачи осуществляется с помощью линейной модели. Разумеется, такая постановка не является единственно возможной. Некоторые пути для дальнейшего развития метода предлагаются в следующих параграфах главы. Причем часть из рассмотренных здесь проблем, например, барьерные точки для налоговых ставок и барьерные точки в условиях неопределенности, до сих пор не обсуждалась в финансовой литературе. Заметим, что до недавнего времени метод барьерной точки применялся в статическом варианте. Экономические показатели рассматривались в рамках одного, сравнительно короткого периода. В последнее время делаются попытки применить метод к потокам платежей, охватывающим ряд последовательных временных интервалов. В этих случаях с помощью дисконтирования стал учитываться важнейший фактор — время (а именно сроки инвестирования и сроки отдачи от инвестиций). Для начала рассмотрим наиболее простой и весьма условный вариант статической постановки задачи, к которому обычно прибегают при объяснении сути метода. Пусть необходимо найти критический объем производства одного вида продукта при условии, что все необходимые для анализа количественные зависимости описываются линейными выражениями, иначе говоря, применяется линейная модель. Для записи такой модели примем обозначения: Q — объем производства в натуральном или условно-натуральном измерении; F — постоянные производственные затраты, затраты, не зависящие от объема выпуска; с — пропорциональные затраты (в расчете на единицу продукции); p — цена единицы продукции; S — общая сумма затрат; V — стоимость выпущенной продукции; P — размер прибыли до уплаты налогов. Переменные Q, F, S, V, Р определяются в расчете на одинаковый интервал времени, обычно на один год. Для начала найдем стоимость выпущенной продукции и соответствующую сумму затрат: V = pQ; (3.1) S = F + cQ. (3.2) Искомый критический объем производства или барьерную точку (break-even point) получим на основе равенства стоимости выпущенной продукции и суммы затрат: V = S. Именно равенство двух разнородных экономических показателей, каждый из которых является функцией управляющего параметра (в рассматриваемом случае — объема производства), лежит в основе метода барьерной точки. Обозначим барьерный объем производства Qk. Тогда, используя (3.1) и (3.2), получим pQk = cQk + F. Таким образом,
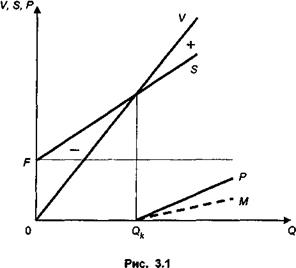
Как видим, значение барьерной ставки пропорционально постоянным затратам и обратно пропорционально разности цены и величины переменных затрат. При уменьшении этой разности величина барьерной точки ускоренно возрастает. Прибыль (до выплаты налогов) по определению составит: P = V - S = (p - c) Q - F. (3.4) Графическая иллюстрация постановки задачи и ее решения приведена на рис. 3.1. Решение находится в точке пересечения двух линий, одна из которых характеризует динамику затрат S, другая — изменение дохода V по мере увеличения выпуска. Объемы производства, которые меньше критического Qk,приведут к убыткам. Превышение этого объема дает прибыль (линия P). Чем выше размер постоянных и переменных затрат, тем больше критический объем производства. Прибыль после уплаты налогов (пропорциональных прибыли) характеризуется на рис. 3.1 пунктирной линией M.
|

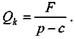 (3.3)
(3.3)