ПРИМЕР 1. Графическое изображение условий задачи и ее решение представлены на рис
Ожидается, что р = 50, с = 30, F = 100. Находим
Графическое изображение условий задачи и ее решение представлены на рис. 3.2.
Рассмотренный метод базируется на реальных данных бухгалтерского учета или ожидаемых их величинах. Капиталовложения учитываются посредством включения в затраты амортизационных отчислений. Заметим, что все участвующие в расчете параметры рассматриваются как константы. Между тем с течением времени они, безусловно, изменяются, и найденная для одного момента времени критическая точка не окажется таковой для другого момента. Важно также подчеркнуть, что время как важнейший финансовый фактор не принимается здесь во внимание. Такой подход вполне оправдан, если капиталовложения уже осуществлены и встает вопрос только о выборе видов производимой продукции и их объемов. Сказанное выше позволяет сформулировать общее определение для обсуждаемого метода как способа расчета барьерного значения управляющего параметра исходя из равенства двух "конкурирующих" функций этого параметра. Содержание управляющего параметра и функций, как видим, определяется конкретными условиями решаемой задачи. В рассмотренном примере управляющим параметром является объем производства, "конкурирующими" функциями — доход (выручка) и затраты. Вариантом рассмотрения задачи является определение минимально допустимого срока выпуска продукции при заданных годовых объемах производства, т. е. срока окупаемости. Объем производства выступает здесь как параметр, а срок выпуска — как управляющая переменная. Вместо годовых постоянных затрат учитывается общий размер инвестиций и сопряженных затрат (параметр F). Тогда "конкурирующие" функции имеют вид V = nQp; S = F + nQc, где n — срок выпуска. Барьерный срок окупаемости nk (методы расчета срока окупаемости для разных ситуаций рассматриваются в гл. 6) определяется как
|

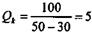 , Р = (50 - 30) Q - 100.
, Р = (50 - 30) Q - 100.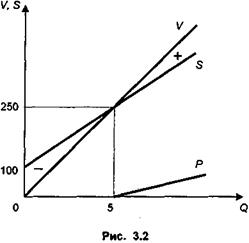
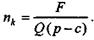 (3.5)
(3.5)


