ПРИМЕР 3. В приведенной ниже таблице и на диаграмме (рис
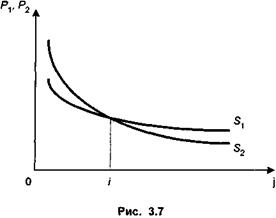
В приведенной ниже таблице и на диаграмме (рис. 3.6) содержатся данные о затратах, стоимости продукции и ожидаемой прибыли.
Барьерный выпуск равен 5. Наибольшая прибыль приходится на выпуск, равный 20.
Сравнение финансовых показателей на основе барьерных величин. Перейдем к решению простой задачи, иллюстрирующей возможности метода при решении некоторых проблем в финансово-кредитной области. Допустим, необходимо выбрать один из двух вариантов поступлений денежных средств: S 1; S 2со сроками n 1; n 2, причем S 2 > S 1; п 2 > n 1, иначе постановка задачи не имеет экономического смысла — выбор очевиден. Решение основано на сравнении величин современной стоимости соответствующих денежных сумм. Таким образом, выбор зависит от существующего или ожидаемого уровня доходности денежных инвестиций ввиде процентной ставки (управляющая переменная j). При выборе варианта следует ориентироваться на значение барьерной ставки[14], т. е. ставки, при которой оба варианта оказываются равноценными по доходности. Рассмотрим метод решения этой задачи для двух вариантов расчета современных стоимостей по простой и сложной процентным ставкам. Для определения барьерных уровней ставок найдем равенства "конкурирующих" функций — современных стоимостей двух платежей P 1 = P 2. Для простой ставки имеем
а для сложной —
где i — величина барьерной ставки. Решив равенство (3.7), получим
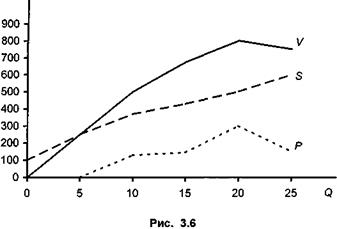
Из выражения (3.9) находим необходимое условие для существования барьерной ставки: S 1 n 2 > S 2 n 1, или Графическая иллюстрация решения представлена на рис. 3.7.
Как видно на рис. 3.7, при j < i предпочтителен вариант S 2
|

 (3.7)
(3.7)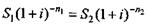 , (3.8)
, (3.8)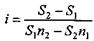 (3.9)
(3.9) .
.