ПРИМЕР 6
Пусть для некоторого производства получены следующие исходные данные: р = 20%, а = 30% (соответственно g = 0,5). Налоговые ставки, допустим, составляют: Т= 25%, N= 21,5%. На основе приведенных выше данных получим: налог на прибыль рТ = 0,2 х 0,25 = 0,05, НДС определяется как gN = (0,2 + 0,3) х 0,215 = 0,1075. Предельное значение параметра g, при котором прибыль полностью идет на налоги, равно согласно (3.15) величине: g = Общая сумма налогов равна 0,1575. Таким образом, двойное начисление налогов сокращает чистую прибыль до 0,0425. Эту же величину можно найти по формуле (3.14) m = 0,2 - [0,2 х (0,25 + 0,215) + 0,3 х 0,215] = 0,0425. Таким образом, прибыль фактически облагается по ставке D = 0,25 + 0,215 + Рассчитаем чистый доход по этой ставке: m = 0,2 х (1 - 0,7875) = 0,0425. Как видим, эквивалентная налоговая ставка на 0,3225 больше суммы исходных ставок. В итоге в распоряжении предприятия при заданных налоговых ставках и сложившейся структуре цены продукции остается меньше 22% прибыли. Продолжим пример. Допустим, речь идет о предприятии с высокими производственными трудозатратами, в связи с чем отношение g/p равно не 2,5, а 3,5. Тогда D = 0,25 + 3,5 х 0,215 > 1, т. е. эквивалентная налоговая ставка оказывается больше 100% и, следовательно, расчетная сумма налогов превышает прибыль. Перейдем теперь к определению барьерных (критических) налоговых ставок. Под последними будем понимать такие расчетные размеры ставок Т или N, при которых чистая прибыль равна нулю при всех прочих заданных условиях; иначе говоря, налоги равны прибыли. Из сказанного следует, что для сохранения экономического смысла налоговые нормативы должны быть меньше соответствующих барьерных ставок. Для решения этой задачи вернемся к уравнению (3.17), определяющему ставку D. Очевидно, что в нормальных экономических условиях должно выполняться неравенство D < 1, или в развернутой записи:
Приведенное неравенство определяет область допустимых с экономической точки зрения сочетаний размеров налоговых ставок. Из него также следует, что налоговые ставки не являются независимыми при условии, что они должны отвечать очевидному экономическому требованию (3.18). Графическая иллюстрация этой области представлена на рис. 3.8. Сплошная наклонная линия здесь соответствует D = 1. Сочетания налоговых ставок, которые лежат на ней, являются предельными (т. е. вся прибыль идет на налоги, например в точке а). Ставки, находящиеся ниже этой линии, позволяют получить некоторую чистую прибыль (точка b).Например, в примере 6 допустимыми являются ставки, удовлетворяющие условию
Рис. 3.8 Барьерные значения ставок можно найти на основе неравенства (3.17) или, что более наглядно, применив уравнение (3.14). Для этого приравняем прибыль после уплаты налогов нулю, тогда p (1 - T) - gN = 0. Если одна из налоговых ставок задана, то для второй можно найти барьерное значение. Обозначим барьерные ставки соответственно как Tk и Nk. Сначала определим барьерную ставку для налога на прибыль. При условии, что заданной является ставка НДС, находим
Ставка налога на прибыль, которая меньше барьерной, создает возможность для получения чистой прибыли. Из приведенного равенства также следует, что положительное значение барьерной ставки существует только тогда, когда Если же Как видим, барьерное значение ставки налога на прибыль является линейной функцией от норматива налога на НДС при заданных параметрах p и g. Аналогичным образом получим барьерное значение ставки НДС при условии, что заданной является ставка налога на прибыль:
Зависимость чистой прибыли от ставки N при заданной ставке T и всех прочих равных условиях показана на рис. 3.9. Как видим, прибыль существует только в диапазоне 0 — а ставки N. Размеры ставки, превышающие критический уровень, приводят к расчетной отрицательной прибыли.
Рис. 3.9
|

 = 0,698, что несколько превышает фактическое его значение, следовательно, имеется чистая прибыль.
= 0,698, что несколько превышает фактическое его значение, следовательно, имеется чистая прибыль. х 0,215 = 0,7875.
х 0,215 = 0,7875. (3.18)
(3.18)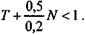

 (3.19)
(3.19) .
. ,то для налога на прибыль не остается "жизненного пространства", вся прибыль идет на НДС.
,то для налога на прибыль не остается "жизненного пространства", вся прибыль идет на НДС. (3.20)
(3.20)



