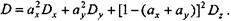ПРИМЕР 2. Вернемся к данным примера 1 и определим структуру портфеля с минимальной дисперсией
Вернемся к данным примера 1 и определим структуру портфеля с минимальной дисперсией. Напомним, что При полной положительной корреляции расчетные значения доли первой бумаги составят по формуле (4.15)
Соответственно ау < 0. Следовательно, минимальная дисперсия имеет место в случае, когда портфель состоит из одной бумаги вида X. Средний доход от портфеля равен 2. При полной отрицательной корреляции находим аx = ay = 1 - 0,579 = 0,421. Дисперсия в этом случае равна нулю (рис. 4.4), а средний доход составит 2,421. При отсутствии корреляции получим по формуле (4.12) ах = 0,654; ау = 1 - 0,654 = 0,346. Дисперсия дохода при такой структуре портфеля равна 0,418, а средний доход — 2,346. Пусть теперь портфель состоит из трех видов бумаг — X, Y, Z. Их доли ах, ау и az = 1 - (ax + ay).Дисперсия дохода от портфеля при условии независимости доходов от отдельных видов бумаг составит:
Минимум дисперсии достигается, если структура портфеля определяется следующим образом:
Не будем останавливаться на ситуации, когда доходы трех видов бумаг статистически зависимы. Перейдем к общей постановке задачи и определим структуру портфеля с n составляющими. Положим, что доходы статистически независимы. Опустим доказательства (см. § 4.4) и приведем результат в матричном виде: A = D -1 e, (4-17) где e — единичный вектор, характеризующий структуру портфеля.
где А — вектор, характеризующий (п - 1) элементов структуры портфеля. Матрица D имеет размерность (n - 1) х (п - 1).
|

 = 0,8;
= 0,8;  = 1,1.
= 1,1. .
. = 0,579;
= 0,579;