СРЕДНЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ31. Исследовать сходимость ряда 32. Исследовать сходимость ряда 33. Исследовать сходимость ряда: 34. Исследовать сходимость ряда: 35. Исследовать на абсолютную или условную сходимость 36. Исследовать сходимость ряда 37. Исследовать сходимость знакочередующегося ряда 38. Найти область сходимости степенного ряда 39. Найти область сходимости степенного ряда 40. Найти интервал сходимости и исследовать сходимость на концах интервала 41. Разложить в ряд Тейлора функцию y=
Элементы гармонического анализа. 42. Является ли функция 43. Является ли функция 44. Найти период функции 45. Написать закон гармонических колебаний с амплитудой 5, частотой 2 и начальной фазой 46. Разложить в ряд Фурье функцию f(x) =1 при 0 47. Разложить в ряд Фурье функцию y = 48. Разложить функцию в ряд Фурье (при необходимости продолжив её периодически на всю числовую ось) y=x -1, -2 <x 49. Разложить функцию 50. Разложить функцию в ряд Фурье, построить амплитудный и фазовый спектры функции f(x) = 51. Представить интегралом Фурье функцию
МИНИСТЕРСТВО ЗДРАВООХРАНЕНИЯ СТАВРОПОЛЬСКОГО КРАЯ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ СРЕДНЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
|
.
.
.
.
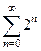, найти область сходимости ряда
периодической?
периодической?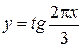
.
.
П и f(-x) = -f(x).
на (-П,П)
2
на промежутке (-П, П] в ряд Фурье, найти и построить амплитудный и фазовый спектры функции
