Собственные и примесные полупроводники

Собственный полупроводник. Рассмотрим механизм проводимости полупроводниковых материалов на примере элементарных полупроводников. В кристалле кремния (он находится в четвертой группе таблицы Менделеева) четыре валентных электрона каждого атома образуют четыре ковалентные связи. Каждая связь образована двумя электронами, принадлежащими соседним атомам, - рис. 2.1. В узле решетки находится ион кремния с зарядом +4, ему принадлежат четыре валентных электрона (электроны изображены черными точками). В идеальном полупроводнике, изображенном на рис. 2.1.а, все электроны связаны. Если такой полупроводник поместить в электрическое поле, то ток через него не потечет, так как нет свободных носителей заряда. Если под внешним энергетическом воздействии (например, тепловом) произойдет разрыв валентной связи, то электрон станет свободным и сможет двигаться в электрическом поле. Такой процесс называется генерацией. На месте электрона остается незанятая связь, имеющая избыточный положительный заряд, так как он не скомпенсирован зарядом электрона. Вакантное место в ковалентной связи называется дыркой. В целом кристалл остается электронейтральным. На рис. 2.1.б свободные электроны и дырки изображены темными и светлыми кружками. Если свободный электрон вернется к своему атому в ковалентную связь, то он будет связанным. Такой процесс называется рекомбинацией.

Вакантное место в ковалентной связи – дырка будет перемещаться во внешнем электрическом поле, что равносильно перемещению по полю положительного заряда, а отрицатель-

но заряженный электрон двигается против поля. Механизм проводимости, обусловленный движением связанных электронов по вакантным связям, называется дырочной проводимостью.

Полупроводник, в котором в результате разрыва ковалентных связей образуется равное количество свободных электронов и дырок, называется собственным. Энергия, необходимая для разрыва ковалентной связи, называется шириной запрещенной зоны полупроводника – E_g.

 

 

Рис. 2.1. Ковалентные связи в собственном полупроводнике (кремнии)

 

Ширина запрещенной зоны является важнейшей характеристикой полупроводника, например, для кремния она равна E_g = 1,1 эВ, для германия – 0,66 эВ, для арсенида галлия – 1,43 эВ. Единица измерения 1 эВ соответствует энергии электрона, ускоренного разностью потенциалов в 1 В, поэтому 1 эВ = 1,6 ∙ 10^-19 К ∙ 1 В = 1,6 ∙ 10^-19 Дж.

При комнатной температуре концентрация свободных электронов и дырок в германии равна 10¹³ см^-3, в кремнии –

10¹⁰ см^-3. С ростом температуры увеличивается число разорванных связей, и концентрация свободных электронов и дырок растет по экспоненте. При приложении электрического поля свободные электроны и дырки (носители заряда) двигаются под воздействием поля, их направленное движение называется дрейфом.

Важной характеристикой полупроводникового материала является подвижность носителей заряда 𝜇. Она численно равна скорости дрейфа v носителей заряда в электрическом поле единичной напряженности

 

μ = , (2.1)

 

где Е – напряженность электрического поля. Подвижность электронов μ_n и дырок μ_p разные: μ_n > μ_p практически во всех полупроводниках. Чем выше подвижность носителей заряда в полупроводнике, тем более быстродействующие приборы можно изготовить на его основе, тем лучше будет его электропроводность.

В чистом полупроводнике, не содержащем примесей, осуществляется электронная и дырочная проводимость. Электрический ток в собственном полупроводнике складывается из двух составляющих – электронного и дырочного токов, текущих в одном направлении.

Прохождение тока в веществе подчиняется закону Ома I = U/R, где U – разность потенциалов на концах проводника, а R – его сопротивление. В дифференциальной форме закон Ома связывает плотность тока j с электропроводностью σ и напряженностью электрического поля Е:

 

j = σ ∙ E. (2.2)

 

 

Электропроводность σ является обратной величиной удельному сопротивлению ρ

σ = . (2.3)

 

Электропроводность (или проводимость) зависит от концентрации носителей заряда и их подвижности. Поскольку ток в собственном полупроводнике переносится электронами и дырками, то и электропроводность собственного полупроводника σ_i имеет два слагаемых:

 

σ_i = e ∙ n_i ∙ μ_n + e ∙ p_i ∙ μ_p, (2.4)

 

где e – заряд электрона, n_i и p_i – концентрация электронов и дырок. Индекс i показывает, что параметры относятся к собственному полупроводнику (intrinsic английское слово - собственный). В собственном полупроводнике n_i = p_i

 

σ_i = e ∙ n_i ∙ (μ_n + μ_p). (2.5)

 

Электропроводность σ_i зависит от ширины запрещенной зоны Е_g и температуры Т:

 

σ_i = σ_{0 ∙} exp [- E_g/(2kT)], (2.6)

 

где σ₀ – предэкспоненциальный множитель, слабо зависящий от температуры, k – постоянная Больцмана.

 

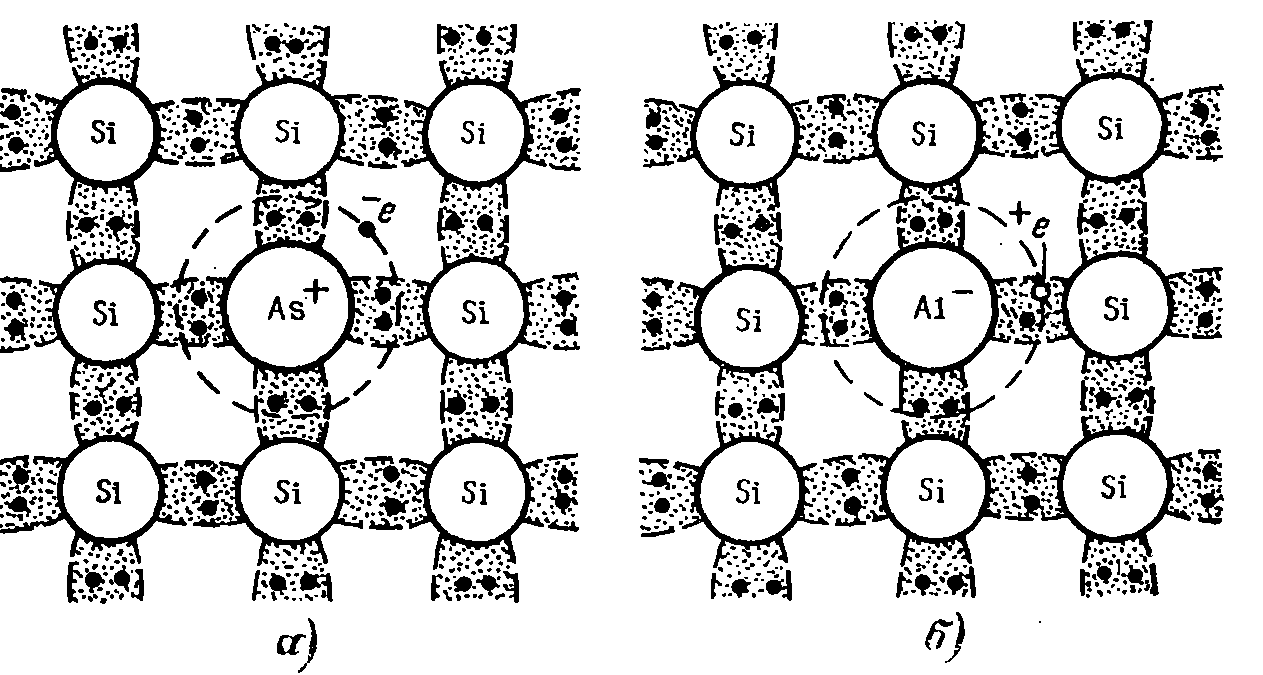
Примесный полупроводник. Рассмотрим электропроводность элементарного полупроводника, в котором один из атомов замещен элементом пятой группы, например, мышьяк в кремнии. Полупроводник, имеющий примеси, называется примесным, а проводимость, созданная примесью, называется примесной.

У мышьяка пять валентных электронов. В решетке кремния четыре валентных электрона мышьяка участвуют в образовании ковалентной связи – рис. 2.2.а. Пятый электрон в ковалентную связь не вступает, он электрически связан с атомом мышьяка (уравновешивает его заряд), но эта связь намного слабее ковалентной. При низких температурах пятый электрон локализован около атома мышьяка, но при повышении температуры он отрывается от атома примеси и может свободно двигаться по кристаллу, а атом мышьяка превращается в положительный ион.

Энергия отрыва пятого электрона от атома примеси ∆Е_пр намного меньше энергии отрыва электрона из ковалентной связи ∆Е_пр ≪ Е_g. ∆Е_пр называется энергией активации примеси. ∆Е_пр в кремнии и германии составляет сотые доли электроновольта. Например, ∆Е_пр для мышьяка в кремнии составляет 0,05 эВ.

 

 

Рис. 2.2. Кристаллическая решетка донорного (а)

и акцепторного (б) полупроводников

 

Вместе с ионизацией примеси может происходить и ионизация основного вещества. Но при не очень высоких температурах количество электронов, оторванных от примеси, будет на порядки больше количества свободных электронов и дырок, образовавшихся за счет разрыва ковалентных связей. Поэтому в таком полупроводнике количество электронов n будет намного больше количества дырок p, такой полупроводник называется электронным или n-типа, а примесь, отдающая электроны, называется донорной.

Донорными примесями в германии и кремнии являются элементы пятой группы таблицы Менделеева: сурьма, фосфор, мышьяк.

Электроны в полупроводнике n-типа называются основными носителями заряда, а дырки – неосновными.

При комнатной температуре в кремнии и германии вся примесь ионизирована, каждый атом примеси отдал один электрон, поэтому концентрация свободных электронов n равны концентрации примеси N_пр: n = N_пр, а формулу (2.4) можно записать в виде

 

σ = e ∙ n ∙ μ_n + e ∙ р ∙ μ_p, (2.7)

 

учитывая, что p ≪ n,

 

σ = e ∙ n ∙ μ_n = σ = e ∙ N_пр ∙ μ_n. (2.8)

 

Если в качестве примеси в кристаллическую решетку полупроводника с ковалентной связью ввести атомы элементов третьей группы таблицы Менделеева, например, алюминий в решетку кремния, то одна ковалентная связь не будет полностью заполнена – рис. 2.2.б. В незаполненную связь около атома алюминия может перейти электрон от атома кремния, при этом образуется отрицательный ион алюминия

и свободная дырка, которая перемещается по связям кремния и принимает участие в проводимости полупроводника.

Примесь, захватывающая электроны, называется акцепторной. В этом случае для образования свободной дырки требуется значительно меньшая энергия (энергия активации примеси) ∆Е_пр, чем для разрыва ковалентных связей кремния: ∆Е_пр ≪ Е_g. Поэтому количество дырок р будет значительно больше количества свободных электронов n и электропроводность кристалла будет дырочной. В таком полупроводнике основными носителями будут дырки, а электроны - неосновными носителями. Полупроводник с акцепторной примесью называется дырочным или р-типа.

Типичными акцепторами в кремнии и германии являются элементы третьей группы таблицы Менделеева: бор, алюминий, галлий. ∆Е_пр акцепторов в кремнии и германии имеет такой же порядок величины, как и ∆Е_пр доноров, и составляет сотые доли электроновольта. Для алюминия в кремнии она составляет ∆Е_пр = 0,06 эВ.

Для электропроводности такого полупроводника, учитывая p ≫ n, формула (2.7) примет вид

 

σ = e ∙ p ∙ μ_р = σ = e ∙ N_пр ∙ μ_р. (2.9)

 

При низких температурах, когда тепловой энергии kT недостаточно для полной ионизации примеси (kT≪ ∆Е_пр ) проводимость примесного полупроводника с ростом температуры будет экспоненциально расти

 

σ_пр = σ_{0 ∙} exp [- ∆ E_пр/(2kT)]. (2.10)

 

Последняя формула одинакова для электронных и дырочных полупроводников.

На этом температурном участке происходит активация примеси, концентрация основных носителей в примесном по-

лупроводнике с ростом температуры растет по экспоненте; этот участок называется участком примесной проводимости.

Температурный участок, на котором примесь полностью ионизирована (концентрация основных носителей равна N_пр), а собственная проводимость σ_i ≪ σ_пр, называется участком истощения примесной проводимости. Для этого участка можно считать, что с ростом температуры проводимость практически не изменяется σ_пр = e ∙ μ_пр ∙ N_пр ≈ const, так как μ_пр слабо зависит от температуры.

При дальнейшем повышении температуры, когда концентрация собственных носителей заряда n_i становится сравнимой с N_пр, начинается участок собственной проводимости, для которого справедлива формула (2.6). Таким образом, при высоких температурах все примесные полупроводники становятся собственными (при этом исчезают разница между полупроводниками n- и р-типа).

Температура перехода к собственной проводимости зависит от ширины запрещенной зоны полупроводника и от концентрации примеси. Чем больше ширина запрещенной зоны, тем при более высоких температурах наблюдается собственная проводимость.