Перешикування відділення

Дата добавления: 2015-08-29; просмотров: 814

Интенсивность излучения лучистого потока, распространяющегося от источника в веществе по направлению l, при постоянном коэффициенте поглощения и отсутствии собственного излучения вещества, определяется законом Буггера –Ламберта:

I = I_o exp (-kl). (3.11)

Эта формула соответствует интенсивности монохроматического лучистого потока в единице телесного угла. Для того чтобы получить полное значение плотности теплового потока, приходящего в данную точку со всех направлений и во всем диапазоне частот излучения, необходимо суммировать это выражение по пространственному углу и частотам:

q_л._х = ;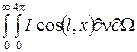

q_л._y = 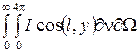; (3.12)

q_л._z = .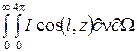

Общий вектор плотности теплового потока лучистой энергии определяется через сумму его проекций на координатные оси:

q_л= q_лхi+q_лyj + q_л.z k. (3.13)

При радиационном теплообмене тело, имеющее температуру Т₁, отдает тепло путем излучения менее нагретому телу с температурой Т₂. В соответствии с законом Стефана-Больцмана плотность теплового потока прямо пропорциональна разности четвертых степеней температур:

q = s_пр 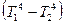, (3.14)

где s_пр – приведенный коэффициент лучеиспускания.

Величина s_пр зависит от геометрической формы, размеров и взаимного расположения тел, а также от свойств поверхностей (степени черноты). Строгий учет всех этих факторов в каждом конкретном случае представляет собой сложную задачу. Однако при небольшой разности температур Т₁ и Т₂ можно приближенно положить:

q = a_л 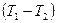. (3.15)

Это выражение аналогично закону Ньютона для конвективного теплообмена. Величина a_л называется коэффициентом лучистого теплообмена и измеряется в тех же единицах, что и a. Для определения a_л также в основном используются экспериментальные методы.

3.1.3. Определение температурного поля

Чтобы найти вид функции Т = Т(x, y, z, t), описывающей температурное поле тела, необходимо установить аналитические зависимости температуры от всех влияющих на нее факторов: внешних и внутренних тепловых воздействий, а также формы тела, его размеров, теплофизических свойств. Выявление таких зависимостей возможно, если сформулировано некоторое дифференциальное уравнение.

Такое дифференциальное уравнение можно получить на основе закона сохранения энергии, который для случая передачи теплоты можно сформулировать следующим образом: разность между количествами энергии, входящей в некоторый объем и выходящей из него в единицу времени, равна скорости изменения энергии в этом объеме.

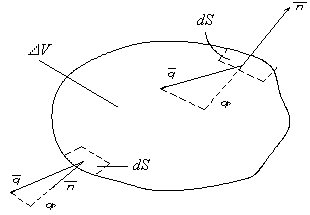
Тепловой баланс (рис.3.2) возможно составить для произвольно выделенного конечного объема вещества DV, ограниченного поверхностью S:

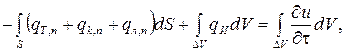(3.16)

где q_Т,п, q_к,п, q_л,п – проекции векторов кондуктивного, конвективного и лучистого плотностей потоков теплоты, проходящих через поверхность dS, на направление нормали n к поверхности; q_И – удельная мощность внутренних источников теплоты, Дж/(м³с); и – объемная плотность энергии, Дж/м³.

Знак «-» перед интегралом по поверхности показывает, что положительными потоками, проходящими через S и увеличивающими объемное количество энергии, являются входящие потоки, т.к. положительным направлением нормали к поверхности принято считать направление наружу.

Преобразование поверхностного интеграла в объемный по теореме Остроградского-Гаусса и переход к пределу DV®0 приводит к дифференциальному уравнению

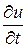+ div (q_т +q_к +q_л )–q_И = 0. (3.17)

Дивергенция или расхождение поля вектора А – скаляр, являющийся объемной производной этого поля:

divА = 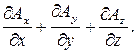(3.18)

В общем случае объемная плотность энергии u включает в себя внутреннюю энергию вещества, кинетическую энергию движения вещества, потенциальную энергию сжатия. При турбулентном переносе теплоты в сумму плотностей потоков добавляется q_турб. Однако в большинстве случаев практически важных процессов теплообмена, не связанных с большими значениями скоростей движения и давлений, с достаточной точностью можно принять

u = rcT. (3.19)

При переносе теплоты только за счет теплопроводности (q_к = q_л = 0) уравнение (3.17) в этом случае будет содержать только q_т –плотность теплового потока теплопроводности. Подставив q_т = -lgrad T, получим

rс 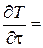div (l grad T) + q_И.

div (l grad T) = l ;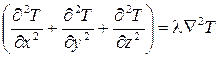

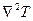– оператор Лапласа;

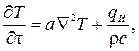(3.20)

где a = l/rc – коэффициент температуропроводности – важная теплофизическая характеристика вещества, определяющая быстроту изменения температурного поля, м²/с.

Полученное дифференциальное уравнение (3.20) описывает нестационарный процесс переноса тепла в неподвижной однородной изотропной среде и называется уравнением теплопроводности.

Рассмотрим вид этого уравнения в некоторых частных случаях, имеющих место на практике.

1. При отсутствии внутренних источников тепла (q_И = 0) нестационарное поле описывается уравнением Фурье:

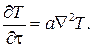(3.21)