
Головна сторінка Випадкова сторінка
КАТЕГОРІЇ:
АвтомобіліБіологіяБудівництвоВідпочинок і туризмГеографіяДім і садЕкологіяЕкономікаЕлектронікаІноземні мовиІнформатикаІншеІсторіяКультураЛітератураМатематикаМедицинаМеталлургіяМеханікаОсвітаОхорона праціПедагогікаПолітикаПравоПсихологіяРелігіяСоціологіяСпортФізикаФілософіяФінансиХімія
Рота у похідному строю
Дата добавления: 2015-08-29; просмотров: 844
|
|
В нестационарных тепловых процессах температура тела зависит от времени. Для однозначного определения этой зависимости необходимо задать начальное условие – распределение температуры в начальный момент времени:
Т ç 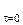 = То. (3.34)
= То. (3.34)
В общем случае температура То является функцией координат То = То(х, у, z). Так как начало времени выбирается произвольно, то в большинстве практических задач можно выбрать момент t = 0, совпадающий с равновесным состоянием. Тогда начальное распределение температуры по объему тела является равномерным и Тo = const, что значительно упрощает решение задачи.
Граничные условия задачи описывают теплообмен внешней поверхности тела с окружающей средой и, таким образом, задают связь между внешними тепловыми воздействиями и температурным полем внутри тела.
Если по условию задачи известна температура поверхности тела, то можно записать граничное условие первого рода (ГУ I рода):
Тлов = Тп. (3.35)
Температура поверхности Тп может быть постоянной величиной (Тп = const) или изменяться во времени: Тп = Тп(t). Граничное условие имеет наиболее простой вид для тел канонической формы в случае одномерного теплового потока. Например,
Тú 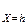 = Тп; Тú
= Тп; Тú 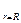 = Тп.
= Тп.
Во многих задачах известна мощность, подводимая извне (или отводимая) к поверхности тела. Для характеристики такого вида теплового воздействия применяется граничное условие второго рода (ГУ II рода). Это условие получается путем приравнивания плотности теплового потока, определяемой законом Фурье у поверхности тела, к поверхностной мощности внешнего источника тепла qs:
±l(gradT)пов = qs. (3.36)
При записи ГУ II рода необходимо обратить внимание на правило знаков. Величина l(gradT)пов записывается с минусом, если соответствующая ось координат направлена внутрь тела; в противном случае знак «+».
Поверхностная мощность qs положительна в случае подвода тепла и отрицательна в случае отвода (рис 3.5):
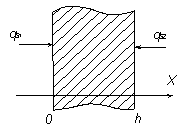
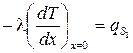 ;
; 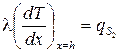 .
.
Если на поверхности тела имеется идеальная тепловая изоляция, то qs = 0 (адиабатическое условие), и, следовательно, (grad T)пов = 0.
 Граничное условие третьего рода (ГУ III рода) описывает конвективный теплообмен поверхности тела со средой, имеющей температуру Тс (рис. 3.6). Приравнивая величину плотности теплового потока, подводимого к поверхности путем теплопроводности, к величине плотности теплового потока, определяемой законом Ньютона для конвективного теплообмена, получим
Граничное условие третьего рода (ГУ III рода) описывает конвективный теплообмен поверхности тела со средой, имеющей температуру Тс (рис. 3.6). Приравнивая величину плотности теплового потока, подводимого к поверхности путем теплопроводности, к величине плотности теплового потока, определяемой законом Ньютона для конвективного теплообмена, получим
±l(gradT)пов = a[Tc-(T)пов]. (3.37)
Правило знаков такое же, как и в случае ГУ II рода. Например,
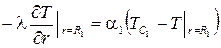 ;
; 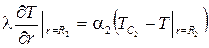 .
.

 При конвективном теплообмене внешнее тепловое воздействие характеризуется уже не одним, а двумя параметрами: температурой среды Тс (постоянной или меняющейся во времени) и коэффициентом теплообмена a. При малых значениях коэффициента теплообмена (a®0) ГУ III рода переходит в адиабатическое условие второго рода. Если же коэффициент теплообмена очень велик (a®¥), то температура поверхности становится равной температуре среды, и ГУ III рода переходит в граничное условие первого рода.
При конвективном теплообмене внешнее тепловое воздействие характеризуется уже не одним, а двумя параметрами: температурой среды Тс (постоянной или меняющейся во времени) и коэффициентом теплообмена a. При малых значениях коэффициента теплообмена (a®0) ГУ III рода переходит в адиабатическое условие второго рода. Если же коэффициент теплообмена очень велик (a®¥), то температура поверхности становится равной температуре среды, и ГУ III рода переходит в граничное условие первого рода.
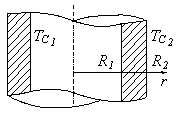
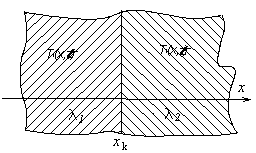
Теплообмен на поверхности идеального контакта двух различных тел описывается граничным условием четвертого рода (ГУ IV рода). На поверхности контакта температура и тепловой поток неразрывны (рис. 3.7). Если одномерные температурные поля двух тел описываются функциями T1(x, t) и T2(x, t), то ГУ IV рода имеет вид
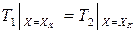 ;
; 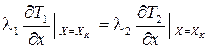 . (3.38)
. (3.38)
 Если тело в одном или нескольких направлениях имеет очень большую протяженность, его приближенно считают бесконечным (полубесконечным). На достаточно большом удалении от источника теплового воздействия его влияние практически не сказывается; поэтому условие на «бесконечности» обычно записывают в виде
Если тело в одном или нескольких направлениях имеет очень большую протяженность, его приближенно считают бесконечным (полубесконечным). На достаточно большом удалении от источника теплового воздействия его влияние практически не сказывается; поэтому условие на «бесконечности» обычно записывают в виде
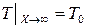 или
или 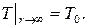 (3.39)
(3.39)
Если сплошное тело имеет плоскость, ось или центр симметрии, а условия теплообмена одинаковы по всей его поверхности, то следует применить условие симметрии. Из равенства температур точек, находящихся на одинаковом расстоянии от центра, оси или плоскости симметрии следует, что температура там должна иметь либо максимальное (в случае охлаждения), либо минимальное (в случае нагрева) значение. Поэтому градиент температуры в этой точке равен нулю:
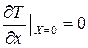 ; или
; или 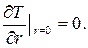 (3.40)
(3.40)
3.1.5. Стационарный режим теплопроводности.
Стационарное температурное поле
В стационарном температурном поле температура не изменяется во времени, т.е. условие стационарности имеет вид 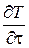 = 0. Процесс теплопроводности при этом описывается уравнением Пуассона или Лапласа.
= 0. Процесс теплопроводности при этом описывается уравнением Пуассона или Лапласа.
Стационарное температурное поле возникает при наличии стационарного теплового режима. Этот режим заключается в постоянстве теплового потока, пронизывающего тело. В частности, если тепловой поток равен нулю, имеет место равновесное состояние, когда температура всех точек тела одинакова. Стационарный тепловой режим предполагает постоянство во времени мощности внутреннего источника тепла (если он есть), а также граничных условий. Так, при ГУ I рода необходимо постоянство температур поверхностей тела, при ГУ II рода – постоянство плотности подводимого теплового потока, при ГУ III рода – постоянство температур окружающих сред и коэффициентов теплообмена.
Пусть в некотором теле установился тепловой режим при наличии внутреннего источника тепла, мощность которого постоянна во времени и равномерно распределена по объему тела (qИv = const). Если тело представляет собой неограниченную пластину (плоская стена), то уравнение Пуассона для одномерного поля имеет вид
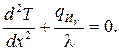 (3.41)
(3.41)
Перепишем это уравнение в виде
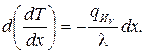
Интегрируя, получим выражение для градиента температуры:
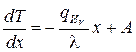 ,
,
где А – постоянная интегрирования.
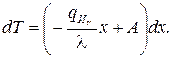
После повторного интегрирования получим функцию, описывающую температурное поле:
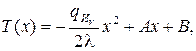 (3.42)
(3.42)
где В – постоянная интегрирования.
Для нахождения постоянных А и В необходимо иметь систему из двух уравнений, которыми являются граничные условия задачи.
Исследуем частные случаи стационарного распределения температуры по толщине пластины.
1. При отсутствии внутреннего источника тепла (qИv = 0)
Т = А х + В; 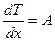 . (3.43)
. (3.43)
Распределение температуры имеет линейный характер, а градиент температуры постоянен по толщине (рис. 3.8). Применим ГУ I рода:
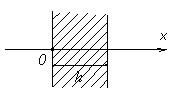
Тú 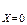 = Т1; Тú
= Т1; Тú 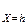 = Т2 , тогда
= Т2 , тогда
T1=B ; 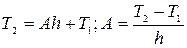 ,
,

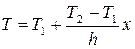 – температурное поле, описывающее распределение температуры в конкретной пластине при qИv = 0.
– температурное поле, описывающее распределение температуры в конкретной пластине при qИv = 0.
Применим закон Фурье qТ = -l grad T;
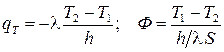 ;
; 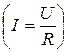 – закон Ома.
– закон Ома.
По аналогии с законом Ома примем RТ = 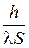 – тепловое (термическое) сопротивление стенки, и Ф =
– тепловое (термическое) сопротивление стенки, и Ф = 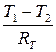 . (3.44)
. (3.44)
Таким образом, если на поверхностях стенки поддерживается определенная постоянная разность температур, то тепловой поток будет тем больше, чем меньше тепловое сопротивление. Если же поддерживается определенный постоянный тепловой поток, то возникающий перепад температур будет тем больше, чем больше RТ.
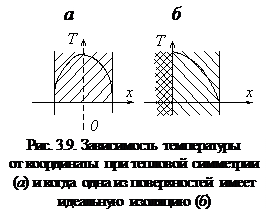 2. Если температурное поле обладает симметрией или одна из поверхностей пластины (х = 0) имеет идеальную тепловую изоляцию, то одно из граничных условий можно записать в виде
2. Если температурное поле обладает симметрией или одна из поверхностей пластины (х = 0) имеет идеальную тепловую изоляцию, то одно из граничных условий можно записать в виде
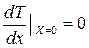 .
.
В этом случае А = 0, и распределение температуры представляет собой квадратичную параболу с вершиной в плоскости х = 0 (рис. 3.9). При отсутствии внутреннего источника и наличии симметрии (или адиабатической поверхности) температура постоянна по толщине пластины (равновесное состояние).
3. Уравнение Пуассона для неограниченного цилиндра или шара, соответственно принимает вид
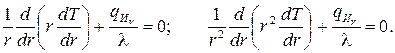 (3.45)
(3.45)
Применяя к этим уравнениям те же процедуры разделения переменных и двукратного интегрирования, получим выражение для температурного поля неограниченного цилиндра:
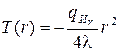 +A ln r + B (3.46)
+A ln r + B (3.46)
и шара:
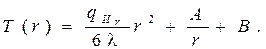 (3.47)
(3.47)
Постоянные интегрирования А и В также определяются граничными условиями задачи.
Одномерное температурное поле сплошного цилиндра обладает осевой симметрией, а сплошного шара – центральной. Условие симметрии в данном случае эквивалентно конечности температуры на оси цилиндра или в центре шара (при r = 0). Для выполнения этого условия необходимо, чтобы постоянная А в том и другом случаях равнялась нулю (в противном случае температура на оси цилиндра или в центре шара стремится к бесконечности, т.к. 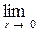 ÷ln r÷®¥;
÷ln r÷®¥; 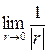 ®¥). Таким образом, стационарное температурное поле сплошных цилиндра и шара описывается квадратичной параболой с вершиной, расположенной на оси цилиндра или в центре шара (рис. 3.10).
®¥). Таким образом, стационарное температурное поле сплошных цилиндра и шара описывается квадратичной параболой с вершиной, расположенной на оси цилиндра или в центре шара (рис. 3.10).
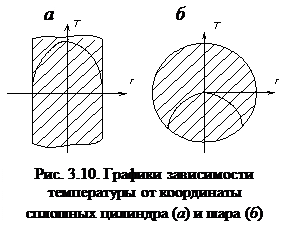 При отсутствии внутренних источников тепла стационарное распределение температуры в этих телах может быть только равновесным.
При отсутствии внутренних источников тепла стационарное распределение температуры в этих телах может быть только равновесным.
Полые цилиндр и шар представляют собой соответственно цилиндрическую и сферическую стенки (рис. 3.11). Положив qИv = 0, видим, что в отсутствие внутренних источников распределение температуры по толщине стенок имеет соответственно логарифмический и гиперболический характер:
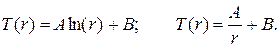 (3.48)
(3.48)
ГУ I рода: 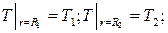
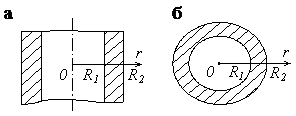
Рис. 3.11. Расчетные схемы для определения температурных полей
в цилиндрической (а) и сферической (б) стенках
T1 = A ln R1+B, T1 = 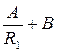 ,
,
T2 = A ln R2 +B, T2 = 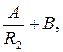
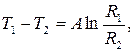
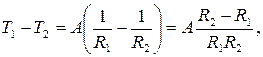
A = 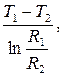 A =
A = 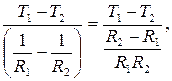
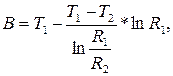 B =
B = 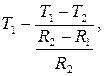
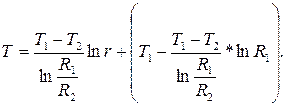
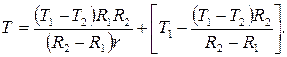
Закон Фурье 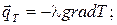
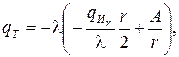
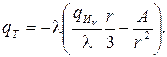
Для стенки, в которой qИv = 0, выражения для теплового потока:
Ф = 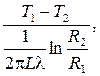
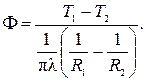
Термическое сопротивление цилиндрической и сферической стенок:
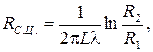
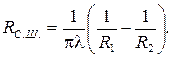
Если 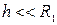 , то
, то 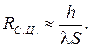 Если
Если 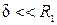 , то
, то 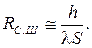
Промышленные способы подвода и отвода теплоты
(теплообмен в химико-технологических аппаратах)
3.2.1. Теплообмен в текучих средах
Проведение реакций между двумя или более реагентами, находящимися в жидком или газообразном состоянии, представляет собой один из наиболее распространенных процессов химической технологии. На полноту химического превращения в реальном реакционном аппарате (реакторе) влияют многие факторы: характер основной химической реакции, то есть зависимость скорости реакции от концентрации реагентов; тепловой эффект реакции; установившаяся в зоне реагирования температура; наличие побочных реакций; подвод (или отвод) теплоты от реакционной массы; количество подаваемых в зону реакции реагирующих веществ и время их пребывания в зоне реакции; характер гидродинамического перемешивания реакционной массы и т.д.
Для полного анализа химических, физико-химических и физических процессов в гомогенном жидкофазном реакторе, когда химическая реакция не сопровождается образованием паровой или твердой фаз, необходимо иметь: 1) стехиометрическое уравнение реакции и константу ее равновесия; 2) уравнения неразрывности всех компонентов с учетом источника (стока) массы за счет химической реакции; 3) уравнение гидродинамики потоков с учетом возможного изменения объемов продуктов реакции; 4) уравнение переноса энергии с учетом источника (стока) теплоты за счет теплоты реакции; 5) уравнение переноса реагирующих компонентов за счет конвективного и диффузионного механизмов, также с учетом стока (источника) массы; 6) кинетическое уравнение химической реакции, определяющее зависимость скорости химического превращения от концентрации реагентов; 7) зависимость константы скорости реакции от температуры и энергии активации (уравнение Аррениуса).
Такая система алгебраических и дифференциальных уравнений с соответствующими начальными и граничными условиями полностью определяет поля температуры, концентраций и скоростей движения реагентов в реакционном аппарате. Усреднение этих полей на выходе из аппарата позволяет получить интегральную степень превращения, достигаемую при заданных условиях работы.
Однако решение общей системы уравнений, описывающей протекающий в реакторе процесс, не представляется возможным ввиду значительной сложности нелинейных дифференциальных уравнений переноса с коэффициентами (вязкость, коэффициенты теплопроводности, диффузии и т.д.), зависящими от искомого распределения температуры.
Как известно, при анализе сложных процессов, нужны приемлемые упрощения их описания. В теории химических реакторов принято полагать, что вместо сложного химического, теплового и диффузионного взаимодействия можно анализировать более простые предельные варианты процессов: 1) скорость собственно химической реакции значительно меньше скорости подачи реагентов в аппарат и транспортировки их из основной массы потока в зону непосредственно реагирования, при этом интегральная скорость всего процесса не зависит от интенсивности массообменных процессов, а определяется кинетикой химической реакции (концентрацией и температурой реагентов) – это так называемая кинетическая область протекания процесса; 2) скорость химической реакции велика, и общий темп химического превращения определяется скоростью транспортировки реагентов в зону реагирования – диффузная область; 3) скорость реакции зависит в сравнимой степени как от диффузионных процессов, так и от кинетики химической реакции – смешанная область.
В некоторых простых случаях быстрого протекания химических и диффузионных процессов общую степень превращения может лимитировать скорость подвода реагентов в реактор (балансовая задача).
Уравнение скорости химической реакции (быстроты изменения концентраций реагентов со временем) записывается в степенной форме относительно концентрации реагентов:
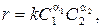 (3.54)
(3.54)
где a1 и a2 – порядки реакции по компонентам 1 и 2, получаемые, как правило, опытным путем; k – константа скорости реакции.
Общепринятой является запись температурной зависимости k в виде уравнения Аррениуса
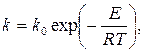 (3.55)
(3.55)
где Е – энергия активации данной реакции; R – газовая постоянная; ko – предэкспоненциальный множитель, зависящий от вероятности реагирования молекул реагентов при их столкновении. Значение ko определяется опытным путем для конкретных реакций, проводимых при разных температурах Т (в К).
При анализе температурных режимов работы реакционных аппаратов принято рассматривать следующие предельные и промежуточные варианты:
1) изотермический режим, при котором постоянство температуры во всем реакционном объеме аппарата поддерживается за счет достаточно интенсивного теплообмена с окружающей средой, позволяющего подводить к реакционной массе (или отводить от нее) всю поглощаемую (или выделяемую) теплоту химической реакции; кроме того, должно быть обеспечено полное перемешивание реагирующей массы, чтобы не было температурных градиентов;
2) адиабатический режим предполагает отсутствие теплообмена между зоной реакции и окружающей средой, при этом выделяющаяся за счет реакции теплота идет на разогрев при экзотермических реакциях, а при эндотермических реакциях происходит охлаждение реакционной массы. В проточных реакторах вытеснения температура увеличивается или падает по длине адиабатического реактора;
3) реальный промежуточный режим соответствует частичному отводу теплоты реакции. При этом за счет изменения интенсивности теплоотвода оказывается возможным регулировать температуру реакционной массы во времени для периодических процессов либо по длине проточного аппарата непрерывного действия;
4) при автотермическом режиме теплота реакции используется для поддержания ее температурного режима. Практически это означает подогрев исходных реагентов продуктами реакции, разогретыми в результате экзотермического процесса.
Из уравнений химической кинетики следует, что температура оказывает наиболее значительное влияние на скорость химической реакции в кинетической области процесса.

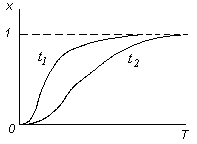 Зависимость степени превращения от температуры для необратимых реакций при некоторых временах процесса реагирования t1 > t2 представлена на рис. 3.13. При фиксированном времени реагирования в случае низкой температуры степень превращения мала. Затем она значительно увеличивается с возрастанием Т, асимптотически приближаясь к полной степени превращения (х = 1). По мере увеличения времени, предоставленного для проведения реакции, можно либо увеличить степень превращения при сохранении температуры реакции, либо уменьшить Т при сохранении необходимой конечной степени превращения. Для проточного реактора увеличение времени реагирования может быть достигнуто увеличением объема реактора или снижением его производительности.
Зависимость степени превращения от температуры для необратимых реакций при некоторых временах процесса реагирования t1 > t2 представлена на рис. 3.13. При фиксированном времени реагирования в случае низкой температуры степень превращения мала. Затем она значительно увеличивается с возрастанием Т, асимптотически приближаясь к полной степени превращения (х = 1). По мере увеличения времени, предоставленного для проведения реакции, можно либо увеличить степень превращения при сохранении температуры реакции, либо уменьшить Т при сохранении необходимой конечной степени превращения. Для проточного реактора увеличение времени реагирования может быть достигнуто увеличением объема реактора или снижением его производительности.

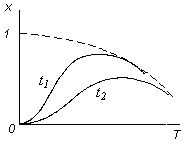 Для обратимых реакций влияние температуры на степень превращения также имеет S-образный характер, но верхний предел кривых соответствует не полной степени превращения, а равновесным концентрациям, зависящим, в свою очередь, от температуры реакции. Кривая равновесия представлена огибающей пунктирной линией (рис. 3.14).
Для обратимых реакций влияние температуры на степень превращения также имеет S-образный характер, но верхний предел кривых соответствует не полной степени превращения, а равновесным концентрациям, зависящим, в свою очередь, от температуры реакции. Кривая равновесия представлена огибающей пунктирной линией (рис. 3.14).
Для экзотермической обратимой реакции определить оптимальную температуру, при которой скорость будет максимальной, можно, если, записав уравнение скорости обратимой реакции, приравнять к нулю производную ¶r/¶T = 0.
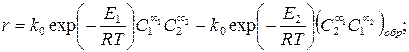 (3.56)
(3.56)
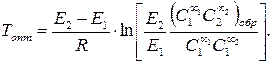 (3.57)
(3.57)
| <== предыдущая лекция | | | следующая лекция ==> |
| Взводу похідному сірою | | | Взвод у розгорнутому строю |