Головна сторінка Випадкова сторінка
КАТЕГОРІЇ:
АвтомобіліБіологіяБудівництвоВідпочинок і туризмГеографіяДім і садЕкологіяЕкономікаЕлектронікаІноземні мовиІнформатикаІншеІсторіяКультураЛітератураМатематикаМедицинаМеталлургіяМеханікаОсвітаОхорона праціПедагогікаПолітикаПравоПсихологіяРелігіяСоціологіяСпортФізикаФілософіяФінансиХімія
СТРОЙОВИЙ ОГЛЯД БАТАЛЬЙОНУ
Дата добавления: 2015-08-29; просмотров: 870
|
|
| Режим течения | Область сопротивления | Закон сопротивления | Пределы области | Формула для λтр |
| Ламинарный | – | hl ~ u | Re < 2300 | 
|
| Турбулентный | Гидравлическая гладкая | hl ~ u1,75 | 
| 
(формула Блазиуса)
|
| Доквадратичная | hl ~ um, m = 1,75÷2 | 
| 
(формула А.Д. Альтшуля)
| |
| Квадратичная | hl ~ u2 | 
(Re  100 000)
| 
(формула Прандтля – Никурадзе)
|
Ламинарное течение в круглой трубе. Плавное изменение скоростей при ламинарном режиме и удобство задания граничных условий (нулевая скорость у стенки) позволяют исследовать ламинарные потоки аналитически. Рассмотрим, например, ламинарное течение в круглой трубе радиуса r0 (рис. 11). Определим силы, действующие на объем жидкости в форме цилиндра радиусом г и длиной l. В направлении оси трубы на торцевые поверхности этого цилиндра действуют силы давления p1πr2 и p2πr2, на боковую поверхность – сила τ2πrl (здесь τ – касательное напряжение трения). Приравнивая эти силы, имеем
.
Поскольку в круглой трубе течение осесимметрично и скорость измеряется только по радиусу, выражение для напряжения трения (I.2а) приобретает вид:
.
Для последних выражения дают дифференциальное уравнение, описывающее поперечное распределение скоростей в трубе:
.
Интегрируя его, имеем
.
Постоянную интегрирования С определим из условия на стенке: u = 0 при r = r0; подставляя в выражение для u, получим формулу Пуазейля (1840):
. (III.2)
Согласно формуле Пуазейля эпюра скоростей в поперечном сечении трубы имеет формулу параболы (рис. 11). Максимальная скорость наблюдается при r = 0, здесь
.
Расход в трубе можно определить интегрированием по сечению трубы элементарных расходов, которые равны произведению скорости (III.2) на площадь элементарного кольца 2πrdr:
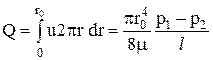. (III.3)
Средняя скорость в трубе
. (III.4)
Из выражения (III.4) легко определить величину гидравлического коэффициента трения λтр в формуле Дарси. Действительно, принимал во внимание, что
, 
, 
,
получаем
. (III.5)
Зависимость (III.5) для коэффициента трения при ламинарном течении в круглой трубе приведена в табл. 3. Она хорошо подтверждается опытом.
| <== предыдущая лекция | | | следующая лекция ==> |
| СТРОЙОВИЙ ОГЛЯД НА МАШИНАХ | | | СТРОЙОВИЙ ОГЛЯД ПОЛКУ |