Стройові огляди офіцерів

Дата добавления: 2015-08-29; просмотров: 925

Прямой удар. При неустановившемся движении жидкости в трубах изменение во времени скорости течения приводит к колебаниям давления, которые называются гидравлическим ударом. Теория этого явления разработана Н. Е. Жуковским (1899). Простейшим случаем гидравлического удара является прямой удар, наблюдаемый при мгновенном перекрытии трубы.

Рассмотрим трубопровод длиной l и сечением S, по которому со скоростью u₀ течет жидкость, находящаяся, под давлением р₀ (рис. 14, а). При резком (мгновенном) закрытии задвижки ближайшие к ней частицы останавливаются. Их кинетическая энергия переходит в работу сжатия жидкости и деформации стенок трубы. Граница раздела сжатого остановившегося объема жидкости – ударная волна – распространяется навстречу втекающей невозмущенной жидкости.

Пусть за время Δt ударная волна проходит путь Δl. Скорость и давление по длине трубы в момент времени, отделенный интервалом Δt от момента закрытия задвижки, представлены графически на рис. 14, б, в. Из рисунка ясно, что ударная волна является поверхностью разрыва для скорости и давления в трубе.

Определим величину ударного давления Δр, т.е. превышение давления в сжатом объеме над невозмущенным давлением р₀. Для этого применим к объему остановленной жидкости SΔl теорему об изменении количества движения:

. (III.9)

Вследствие малой сжимаемости капельных жидкостей и большой жесткости стенок трубы можно считать, что масса жидкости за время Δt внутри остановившегося объема не изменилась; она равна m = ρSΔl. Изменение скорости составляет Δu = u₀ – 0 = u₀. Сила f, вызванная изменением количества движения, есть разность давлений на торцевых поверхностях выбранного объема:

.

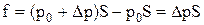Подставляя эти величины в уравнение количества движения (III.9), имеем

.

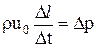Учитывая, что есть скорость распространения ударной волны, получаем формулу Жуковского:

. (III.10)

Отметим, что величина ударного давления при прямом ударе не зависит от длины трубы.

Скорость ударной волны. В трубе с абсолютно жесткими стенками скорость ударной волны равна скорости распространения упругих колебаний (звука). Выведем ее величину.

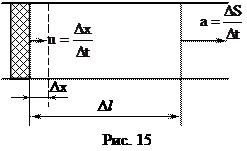Представим себе, что в жидкость, заполняющую трубу (рис. 15) и имеющую модуль объемной упругости Е, вносится возмущение сжатия за счет движения поршня. Пусть за время Δt после начала движения поршень проходит путь Δх. За то же время волна сжатия, которая отделяет невозмущенную, покоящуюся жидкость от начавшей двигаться со скоростью поршня, проходит расстояние Δs. Мы предполагаем, что возмущение слабое, т.е. Δх << Δs.

Сила, с которой поршень сжимает возмущенный объем, пропорциональна его относительному сжатию

. (III.11)

С другой стороны, эту силу можно определить по изменению количества движения в объеме SΔl, применяя уравнение (III.9). Поскольку возмущение слабое, плотность можно считать неизменной и m = ρSΔl. Изменение скорости

.

Следовательно,

,

что совместно с (III.11) дает

.

Но есть скорость распространения волны возмущения в неподвижной жидкости a. Следовательно,

. (III.12)

Исключим из уравнения (III.12) модуль объемной упругости жидкости E. По закону Гука, изменение объема V = SΔl связано с изменением давления Δp соотношением

,

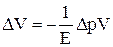или

.

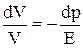Поскольку масса жидкости внутри возмущенного объема не меняется при прохождении волны сжатия (уменьшение объема компенсируется увеличением плотности), очевидно, что ρV = const. Логарифмируя и дифференцируя последнее равенство, получаем

.

Сравнивая с выражением, полученным ранее из закона Гука, имеем

.

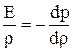по формуле (III.12) скорость звука оказывается равной

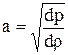. (III.12а)

Как видим, скорость звука зависит от отношения возмущений давления и плотности. Она определяется физическими свойствами жидкости [формула (III.12)]. Для воды, например, скорость звука равна примерно 1420 м/сек, для нефти – около 1200 м/сек.

В случае трубы с деформируемыми стенками скорость ударной волны несколько меньше скорости звука. Она определяется формулой

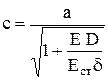, (III.13)

где Е_ст – модуль объемной упругости (модуль Юнга) для материала стенки трубы, D – диаметр, δ – толщина стенки.

* Ламина – слой, пластинка (лат.).

** Турбулентный – бурный, возмущенный (лат.).

* Это эмпирическая формула ЦАГИ. Частный случай резкого сужения – вход в трубу, для которого ζ_вх = 0,5.