
Головна сторінка Випадкова сторінка
КАТЕГОРІЇ:
АвтомобіліБіологіяБудівництвоВідпочинок і туризмГеографіяДім і садЕкологіяЕкономікаЕлектронікаІноземні мовиІнформатикаІншеІсторіяКультураЛітератураМатематикаМедицинаМеталлургіяМеханікаОсвітаОхорона праціПедагогікаПолітикаПравоПсихологіяРелігіяСоціологіяСпортФізикаФілософіяФінансиХімія
ПЕРЕВІРКА І ОЦІНКА СТРОЙОВОЇ ЗЛАГОДЖЕНОСТІ
Дата добавления: 2015-08-29; просмотров: 819
|
|
| Температура, ºС | ν, см2/сек | |
| Вода | Масло турбинное | |
| 0,0179 | 5,20 | |
| 0,0101 | 1,32 | |
| 0,0066 | 0,33 | |
| 0,0048 | 0,146 | |
| 0,0028 | – |
Для определения вязкости капельных жидкостей используются приборы – вискозимерты. Чаще других применяется вискозиметр Энглера, в котором вязкость определяется по времени истечения определенного объема жидкости через калиброванное отверстие.
Сжимаемость. Уменьшение объема при увеличении давления называется сжимаемостью жидкостей. По закону Тука, приращение объема жидкости dV, связанное с приращением давления dp, определяется формулой
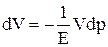 , (I.4)
, (I.4)
где Е – модуль объемной сжимаемости (модуль Юнга) жидкости. Для воды, например, Е = 2,1·104 кгс/см2, для нефти и минерального масла Е ≈ 1,4·104 кгс/см2. Модуль объемной сжимаемости газов зависит от термодинамического характера процесса сжатия; обычно он в тысячи раз меньше, чем для капельных жидкостей (поэтому газы и называют сжимаемыми жидкостями). Наряду с модулем Юнга Е, для характеристики сжимаемости жидкости применяют обратную ему величину – коэффициент сжимаемости 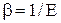 . Как уже упоминалось, капельные, или несжимаемые, жидкости при небольших изменениях давления практически не меняют объема.
. Как уже упоминалось, капельные, или несжимаемые, жидкости при небольших изменениях давления практически не меняют объема.
Поверхностное натяжение. Это механическое свойство капельной жидкости есть следствие действия в жидкости сил сцепления и проявляется в местах соприкосновения жидкости со стенками сосуда. В капиллярных трубах поверхностное натяжение играет существенную роль, в крупных же сосудах и трубопроводах, с которыми приходится иметь дело теплоэнергетике, силы поверхностного натяжения исчезающе малы по сравнению с другими силами.
Тепловое расширение. Тепловое расширение жидкости и связанное с ним изменение плотности при изменении температуры незначительны и обычно не принимаются во внимание в большей части гидравлических расчетов. Тепловое расширение и сжатие газов исследуется технической термодинамикой.
I.2. Основные понятия и уравнения гидростатики
Гидростатика – раздел гидродинамики, изучающий случаи равновесия жидкостей под действием различных сил.
Силы, действующие в жидкости. Механика жидкости и газа рассматривает две категории сил, действующих в жидкости: объемные и поверхностные.
Объемные, или массовые, силы действуют на каждую частицу жидкости внутри данного объема. Таковы силы тяжести и инерции (в том числе центробежная сила). Объемные силы, отнесенные к единице массы жидкости, имеют размерность ускорения. Так, при действии силы тяжести объемная сила численно равна ускорению силы тяжести g; при действии центробежной силы инерции объемная сила равна 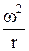 (здесь ω – окружная скорость вращения, r – радиус). Результат действия объемной силы на заданный объем жидкости V выражается ее произведением на массу жидкости внутри данного объема, которая в свою очередь равна произведению объема W на плотность ρ. В итоге действие силы тяжести выражается весом заданного объема gρW, действие центробежной силы равно
(здесь ω – окружная скорость вращения, r – радиус). Результат действия объемной силы на заданный объем жидкости V выражается ее произведением на массу жидкости внутри данного объема, которая в свою очередь равна произведению объема W на плотность ρ. В итоге действие силы тяжести выражается весом заданного объема gρW, действие центробежной силы равно 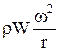 и т.д.
и т.д.
При выборе в жидкости декартовой системы координат xyz рассматривают проекции объемной силы на координатные оси, которые обозначаются прописными буквами X, У, Z и также имеют размерность ускорения. Например, если плоскость xy параллельна поверхности жидкости, ось z направлена вертикально вверх, а на жидкость действует только сила тяжести, то проекции X и Y равны нулю, а проекция Z равна – g (она отрицательна, поскольку сила тяжести действует в направлении, противоположном оси z).
Поверхностные силы действуют на поверхностях, ограничивающих данный объем жидкости от атмосферы, стенок сосуда или соседних объемов жидкости. К поверхностным силам относятся нормальные силы (атмосферное давление, давление со стороны стенок сосуда) и касательные силы, например: касательные напряжения у стенок трубы или у поверхности обтекаемого тела, возникающие при движении жидкости.
Гидростатическое давление в покоящейся жидкости. Сила, действующая со стороны жидкости на единицу площади поверхности тела, соприкасающегося с ней, называется гидростатическим давлением. Если на площадь S действует сила Р, то гидростатическое давление
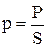 .
.
Если площадь F расположена в жидкости не горизонтально, то в разных ее точках гидростатическое давление оказывается не одинаковым – оно зависит от глубины. В этом случае давление в точке определяется через предельный переход:
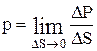 . (I.5)
. (I.5)
Таким образом, гидростатическое давление является напряжению сжатия тела под действием какой-либо силы.
Вектор давления на некоторую площадку, выбранную в жидкости, направлен по внутренней нормали к ней и не зависит от ориентации площадки.
Единица измерения давления в системе СИ – н/м2, в технической системе единиц – кгс/м2. Наиболее распространенная в практике единица давления – кгс/см2 – называется технической атмосферой. Она равна 10 000 кгс/м2 и соответствует давлению столба ртути высотой 735 мм или столба воды высотой 10,00 м. Название «атмосфера» для этой единицы появилось потому, что она по величине близка к среднему атмосферному давлению на уровне моря, равному 1,033 кгс/см2 (давление столб/а ртути высотой 760 мм). В системе СИ производной единицей давления является бар, равный 105 н/м; 1 бар = 1,02 кгс/см2.
Следует отметить, что при сохранении сплошности жидкости давление в ней не может быть ниже некоторого минимума, равного давлению паров данной жидкости, насыщающих пространство при данной температуре. При попытке понизить давление ниже упругости насыщенного пара жидкость вскипает. Ниже приведены данные о давлении насыщения для паров воды при различной температуре.
| Температура, ºС………… | ||||||
| pнас.пар, кгс/см2…………... | 0,006 | 0,024 | 0,075 | 0,200 | 0,480 | 1,033 |
Из приведенных данных следует, например, что при температуре 70° С вода вскипает, если давление на ее поверхности станет менее 0,317 кгс/см2.
Дифференциальные уравнения равновесия жидкости. Вывод дифференциальных уравнений равновесия начнем с частного случая, когда на жидкость действует только сила тяжести и система координат выбрана таким образом, что плоскость ху расположена на поверхности жидкости, а ось h (ось глубин) направлена вертикально вниз (рис. 2).
Рассмотрим условие равновесия жидкости в параллелепипеде с ребрами dx, dy, dh, параллельными координатным осям. Единственной объемной силой, действующей на жидкость внутри параллелепипеда, является сила тяжести g, действие которой выражается весом жидкости – произведением pg dx dy dh. Сила тяжести направлена вертикально вниз, и проекции объемной силы в направлении осей х и у равны нулю. В силу того, что жидкость неподвижна, силы давления на боковые грани взаимно уравновешиваются.
 Рассмотрим проекции сил, действующих на параллелепипед в направлении оси h. Пусть давления на верхней и нижней площадках равны p и p+dp. На верхнюю грань действует сила давления pdxdy, на нижнюю грань – противоположно направленная сила давления (р+dp)dxdy. Просуммировав алгебраически силы давления на верхнюю и нижнюю грань и вес жидкости в объеме параллелепипеда, получим условие равновесия
Рассмотрим проекции сил, действующих на параллелепипед в направлении оси h. Пусть давления на верхней и нижней площадках равны p и p+dp. На верхнюю грань действует сила давления pdxdy, на нижнюю грань – противоположно направленная сила давления (р+dp)dxdy. Просуммировав алгебраически силы давления на верхнюю и нижнюю грань и вес жидкости в объеме параллелепипеда, получим условие равновесия
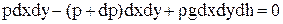 ,
,
или 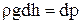 . (I.6)
. (I.6)
Последнее равенство может быть записано также в форме
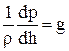 .
.
При произвольной ориентации координатных осей, а также при действии кроме силы тяжести и других объемных сил, приходится учитывать все их проекции X, Y, Z на координатные оси. В этом случае нужно рассматривать изменение давления в направлении всех координатных осей, которое описывается частными производными 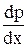 ,
, 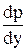 ,
, 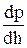 . Пользуясь выводом, аналогичным вышеизложенному, легко получить для этого случая систему дифференциальных уравнений равновесия жидкости Л. Эйлера (1755):
. Пользуясь выводом, аналогичным вышеизложенному, легко получить для этого случая систему дифференциальных уравнений равновесия жидкости Л. Эйлера (1755):
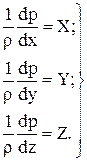 (I.7)
(I.7)
Полный дифференциал гидростатического давления может быть определен из этой системы в результате умножения первого уравнения на dx, второго на dy, третьего на dz и их сложения:
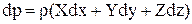 .
.
Интегрирование дифференциальных уравнений гидростатики. Рассмотрим равновесие несжимаемой жидкости под действием, силы тяжести. В дифференциальном уравнении гидростатики (I.6) произведение pg есть удельный вес жидкости γ. Интегрируя уравнение dp = γ dh, имеем
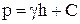 .
.
Постоянная интегрирования С может быть определена с учетом условия на поверхности жидкости: при h = 0 р = р0, следовательно, С = р0. В результате давление p на любой глубине h может быть определено по основному уравнению гидростатики:
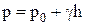 . (I.8)
. (I.8)
В частном случае, когда жидкость имеет свободную поверхность, давление р0 равно атмосферному давлению pа. Таким образом, давление на глубине h (абсолютное давление) складывается из давления на поверхности и давления столба жидкости высотой h – избыточного давления.
Из уравнения гидростатики следует, что давление может измеряться высотой столба жидкости h. На этом основано широкое применение для измерения давления сообщающихся сосудов – пьезометров, жидкостных барометров и манометров, микроманометров. Так, в пьезометре давление внутри сосуда измеряется по высоте подъема h жидкости в открытой трубке; давление на поверхности жидкости в ней равно атмосферному. Очевидно, что 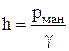 , где манометрическое давление рман = р – ра – есть превышение давления над атмосферным. Давление в сосуде определяется по формуле р = ра + γh. Микроманометр представляет собой пьезометр, в котором измерительная трубка наклонена под небольшим углом к горизонтальной плоскости. Незначительные изменения давления приводят к заметным изменениям длины столбика жидкости в измерительной трубке микроманометра, чем попытается точность измерений.
, где манометрическое давление рман = р – ра – есть превышение давления над атмосферным. Давление в сосуде определяется по формуле р = ра + γh. Микроманометр представляет собой пьезометр, в котором измерительная трубка наклонена под небольшим углом к горизонтальной плоскости. Незначительные изменения давления приводят к заметным изменениям длины столбика жидкости в измерительной трубке микроманометра, чем попытается точность измерений.
Если в пьезометре уровень жидкости расположен ниже уровня в сосуде, слагаемое γh в основном уравнении гидростатики имеет знак минус и называется вакуумом или недостатком давления до атмосферного. Величина, или глубина вакуума в сосуде, измеряется в долях атмосферы или высотах столба жидкости. При вакууме давление не может быть меньше давления паров жидкости, насыщающих пространство при данной температуре. Пьезометр, измеряющий глубину вакуума, называется вакуумметром.
Помимо жидкостных приборов для измерения давления в технике широко используются также механические манометры и вакуумметры – пружинные и мембранные. Давление в них измеряется по величине упругих деформаций чувствительного элемента.
Из уравнения гидростатики непосредственно следует закон Паскаля, согласно которому давление, оказываемое на поверхность покоящейся жидкости, передается всем ее частицам без изменения величины. Действительно, давление на поверхности р0 входит слагаемым в основное уравнение гидростатики, и с его изменением на такую же величину меняется давление внутри жидкости р. На применении закона Паскаля основано устройство гидростатических машин – гидравлических прессов, аккумуляторов и мультипликаторов.
Давление жидкости на стенки. Из определения гидростатического давления (I.5) следует, что сила давления жидкости на стенку может быть найдена суммированием произведений гидростатического давления на величину элементарной площадки или, в пределе, интегрированием сил давления по площади стенки S.
Величина избыточного давления на элементарную площадку dF (рис. 3) равна:
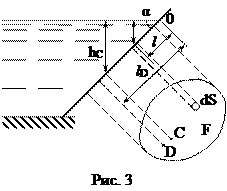
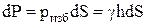 .
.
Сила давления на всю площадку определяется интегрированием элементарного давления по площади F:
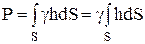 .
.
Но 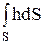 есть статистический момент фигуры S относительно свободной поверхности жидкости, равный согласно выводам теоретической механики произведению площади S на глубину hС погружения центра тяжести фигуры C:
есть статистический момент фигуры S относительно свободной поверхности жидкости, равный согласно выводам теоретической механики произведению площади S на глубину hС погружения центра тяжести фигуры C:
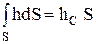 .
.
Таким образом, имеем
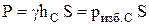 . (I.9)
. (I.9)
где pизб.С – гидростатическое давление в центре тяжести фигуры.
Например, сила избыточного давления на прямоугольный щит шириной b, длиной l, установленной под углом α к поверхности жидкости, будет
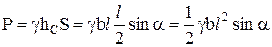 .
.
Выясним, где находится точка приложения равнодействующей сил давления, называемая центром давления.
Определим момент сил давления на стенку относительно линии ее пересечения с поверхностью жидкости. Элементарный момент dМ равен силе давления на элементарную площадку γhdF, умноженной на плечо l (рис. 3):
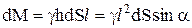 .
.
Суммарный момент сил давления на фигуру определится в результате интегрирования этого выражения по площади F:
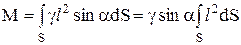 .
.
Выражение 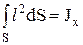 представляет собой момент инерции фигуры F относительно линии поверхности жидкости со стенкой. Итак,
представляет собой момент инерции фигуры F относительно линии поверхности жидкости со стенкой. Итак,
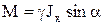 .
.
Но, с дугой стороны, момент инерции М равен произведению равнодействующей сил давления Р на искомое плечо (координату центра давления) lD:
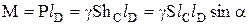 ,
,
здесь lC – координата центра тяжести. Приравнивая полученные выражения для суммарного момента М, определим координату центра давления:
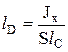 .
.
Представляется целесообразным заменить в полученной формуле момент инерции фигуры относительно линии пересечения поверхности жидкости со стенкой Jx через цент тяжести С параллельно поверхности жидкости, по известной формуле механики
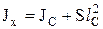 .
.
Тогда
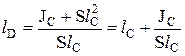 . (I.10)
. (I.10)
Из полученной формулы видно, что центр давления D (рис. 3) лежит ниже центра тяжести С на величину 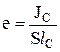 , называемую эксцентриситетом давления. Например, для прямоугольного щита координата центра давления lD равна:
, называемую эксцентриситетом давления. Например, для прямоугольного щита координата центра давления lD равна:
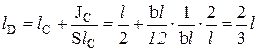
(так как для прямоугольника 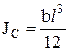 ). Таким образом, точка приложения равнодействующей сил давления на прямоугольную стенку лежит ниже ее центра тяжести на 1/6 l.
). Таким образом, точка приложения равнодействующей сил давления на прямоугольную стенку лежит ниже ее центра тяжести на 1/6 l.
Равнодействующая сил давления на криволинейную стенку может быть определена суммированием сил давления на элементарные площадки, которые можно считать плоскими. Обычно задача определения равнодействующей давления на криволинейную стенку сводится к нахождению ее составляющих по координатным осям.
Определим суммарное давление жидкости на цилиндрическую поверхность АВ с горизонтальной образующей, которая направлена параллельно оси Oy (рис. 4).
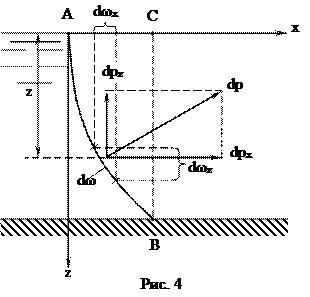
Для этого выделим на поверхности АВ элементарную площадку dω, погруженную под уровень жидкости на глубину z. Суммарное давление dP на эту площадку должно быть направлено по внутренней нормали к площадке и проходит через центр ее тяжести.
Если учитывать только избыточное гидростатическое давление, то суммарное давление определится по формуле dP = γz dω. Разложим это давление на две составляющих – на горизонтальную dPx и вертикальную dPz. Эти составляющие суммарного давления можно будет записать в следующем виде:
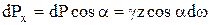 ,
,
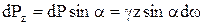 ,
,
где α – угол, составленный суммарным давлением с осью x.
Произведение 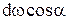 можно рассматривать как проекцию площадки dω на вертикальную плоскость dωz, а
можно рассматривать как проекцию площадки dω на вертикальную плоскость dωz, а 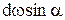 как проекцию площадки dω на горизонтальную плоскость dωx, то есть
как проекцию площадки dω на горизонтальную плоскость dωx, то есть 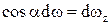 и
и 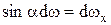 . Подставляя эти выражения в проекцию суммарного давления на оси координат, будем иметь:
. Подставляя эти выражения в проекцию суммарного давления на оси координат, будем иметь:
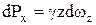 ,
,
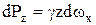 .
.
Для того чтобы получить проекции суммарного давления жидкости на всю цилиндрическую поверхность АВ, проинтегрируем полученные выражения по указанной площади ω.
Тогда будем иметь:
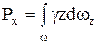 ,
,
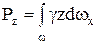 .
.
Рассмотрим выражение для горизонтальной составляющей суммарного давления
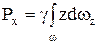 .
.
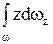 – есть статический момент площади вертикальной проекции цилиндрической поверхности относительно оси y, то есть
– есть статический момент площади вертикальной проекции цилиндрической поверхности относительно оси y, то есть 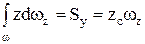 , где zc – расстояние до центра тяжести вертикальной проекции криволинейной поверхности до свободной поверхности жидкости. Следовательно,
, где zc – расстояние до центра тяжести вертикальной проекции криволинейной поверхности до свободной поверхности жидкости. Следовательно,
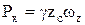 .
.
Горизонтальная составляющая суммарного давления жидкости на цилиндрическую поверхность равна избыточному гидростатическому давлению: в центре тяжести проекции цилиндрической поверхности на вертикальную плоскость, умноженному на величину этой площади. Центр давления горизонтальной составляющей Рх будет определяться так же, как для суммарного давления на вертикальную плоскость
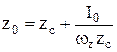 .
.
В данном случае I0 – момент инерции цилиндрической поверхности на вертикальную плоскость относительно центральной горизонтальной оси.
Рассмотрим выражение для вертикальной составляющей суммарного давления жидкости на цилиндрическую поверхность 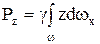 ,
, 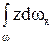 – есть не что иное, как объем призмы АВС, или иначе объем тела давления W, то есть
– есть не что иное, как объем призмы АВС, или иначе объем тела давления W, то есть
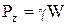 .
.
Телом давления называется объем, ограниченный цилиндрической поверхностью, вертикальной плоскостью, проходящей через нижнюю образующую цилиндрической поверхности, и горизонтальной плоскостью, совпадающей со свободной поверхностью жидкости АС (или ее продолжением).
Таким образом, вертикальная составляющая суммарного давления жидкости на цилиндрическую поверхность Pz равна весу жидкости в объеме тела давления. Тело давления может быть фиктивным, если оно не заполнено жидкость a) и действительным, если оно жидкостью заполнено b) (рис. 5).
Полная величина суммарного давления жидкости на цилиндрическую поверхность может быть выражена геометрической суммой сил Px и Pz и определена по формуле
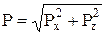 . (I.11)
. (I.11)
 Обе составляющие Px, Pz и их равнодействующая P должны иметь общую точку пересечения. Угол наклона равнодействующей P к горизонту α определится из выражения
Обе составляющие Px, Pz и их равнодействующая P должны иметь общую точку пересечения. Угол наклона равнодействующей P к горизонту α определится из выражения 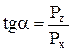 . Точка приложения полной силы давления Р к криволинейной поверхности находится в месте пересечения линии действия силы Р, проходящей через точку, с криволинейной поверхностью.
. Точка приложения полной силы давления Р к криволинейной поверхности находится в месте пересечения линии действия силы Р, проходящей через точку, с криволинейной поверхностью.
Тема II. Основные понятия и уравнения гидродинамики
| <== предыдущая лекция | | | следующая лекция ==> |
| Які перевіряються з одиночної підготовки, та найбільш характерні помилки під час їх виконання | | | ОЦІНКА ВИКОНАННЯ ВИМОГ СТРОЙОВОГО СТАТУТУ В ПОВСЯКДЕННОМУ ЖИТТІ |