ОБЛАДНАННЯ СТРОЙОВОГО ПЛАЦУ

Дата добавления: 2015-08-29; просмотров: 754

Из курса математического анализа известно, что непрерывную функцию, имеющую все непрерывные производные, можно разложить в ряд Тейлора. Поэтому можем для скорости и давления записать следующие разложения

; .

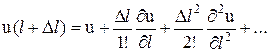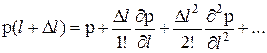Или, пренебрегая малыми величинами высшего порядка, при стремлении Δl к нулю:

; .

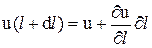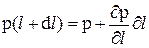Здесь u и 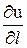скорость и ее первая производная в точке l;

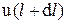– скорость в точке ;

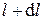p и 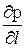– давление и его первая производная в точке l;

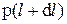– давление в точке .

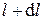Эти разложения мы будем пользоваться в дальнейшем при составлении указанных дифференциальных уравнений.

Выберем в потоке фиксированный в пространстве элементарный объем в форме параллелепипеда с ребрами dx, dy, dz (рис. 7). Пусть у левой грани этого объема составляющая скорости в направлении оси x равна u_x. По достижении правой грани эта составляющая может измениться и стать равной

.

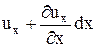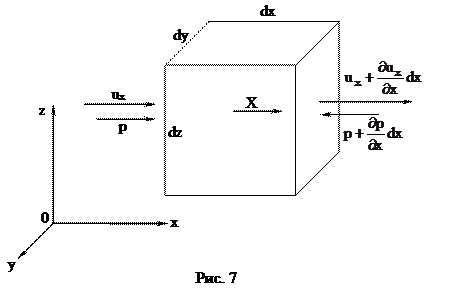
Через левую грань за единицу времени втекает внутрь параллелепипеда объем жидкости, равный произведению нормальной составляющей скорости на площадь грани: w_xdydz.

Через правую грань вытекает объем

.

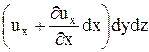Суммарное поступление жидкости через левую и правую грани равно разности:

.

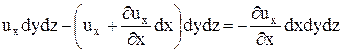Аналогично получим, что через грани, перпендикулярные оси у (задняя и передняя грани на рис. 7), Суммарное поступление жидкости внутрь параллелепипеда равно 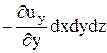. Через грани, перпендикулярные оси z (нижняя и верхняя на рис. 7), поступает объем 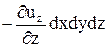. Здесь u_y и u_z – составляющие скорости в направлении осей y и z. Если внутри параллелепипеда нет источников и стоков, т.е. объем жидкости в нем не меняется, то суммарный расход через все грани равен нулю:

.

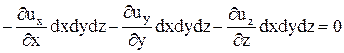Разделив последнее равенство на объем параллелепипеда dxdydz, получим уравнение неразрывности в дифференциальной форме

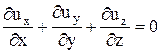. (II.7)

При выводе уравнения неразрывности мы не учитывали сжимаемости жидкости. В наиболее общем случае неустановившегося движения сжимаемой жидкости уравнение неразрывности имеет вид (приводится без вывода):

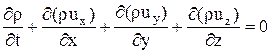. (II.7)