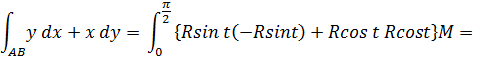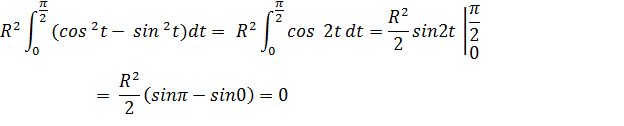1.Если кривая задана уравнением y=y(x) и при перемещении из точки А в точку В x меняется от а до b то

| 
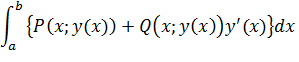 (точки имеют следующие координаты)
(точки имеют следующие координаты)

|
2.Если кривая задана уравнениями x=α (t), y=α (t), и при перемещении из точки A B t меняется от α до β, то
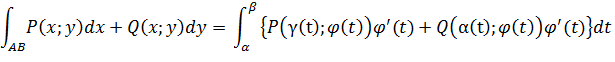
где 
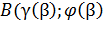
Пример 1. Вычислить криволинейный интеграл второго типа:
 вдоль параболы x=y2 от точки А(1; 1) до В (4; 2).
вдоль параболы x=y2 от точки А(1; 1) до В (4; 2).

| Так как x=y2 dx=2y dy и значение н изменяется от y1=1 до y2=2 при перемещении из точки А(1; 1) в точку В (4; 2), то исходный интеграл вычисляется по формуле:
|
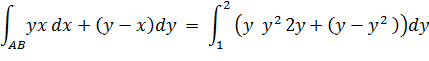
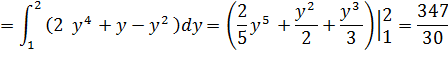
Пример 2
Вычислить криволинейный интеграл второго типа
 вдоль окружения x=Rcos t, y = Rsin t от точки А (R; 0) до точки В (0; R)
вдоль окружения x=Rcos t, y = Rsin t от точки А (R; 0) до точки В (0; R)

| Так как x=R Cos t, y = R Sin t то значение t изменяется от t1=0 до t2= π /2 при перемещении из точки А (R; 0) в точку В (0; R). Найдем дифференциалы переменных x, y: dx= - Rsint dt, dy=Rcostdt
Тогда исходный интеграл вычисляется по формуле:
|
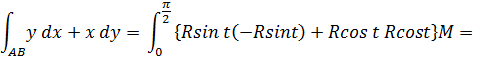
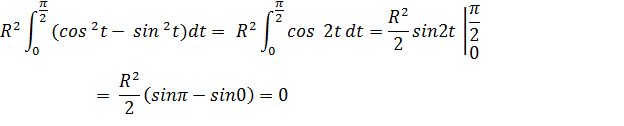



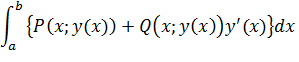 (точки имеют следующие координаты)
(точки имеют следующие координаты)

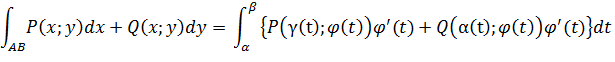

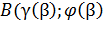
 вдоль параболы x=y2 от точки А(1; 1) до В (4; 2).
вдоль параболы x=y2 от точки А(1; 1) до В (4; 2).
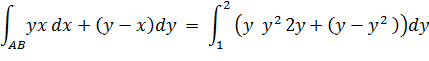
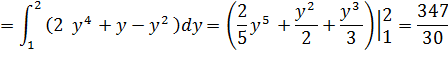
 вдоль окружения x=Rcos t, y = Rsin t от точки А (R; 0) до точки В (0; R)
вдоль окружения x=Rcos t, y = Rsin t от точки А (R; 0) до точки В (0; R)