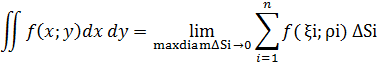Двойной интеграл
Пусть функция Z=f(x, y) задана в некоторой ограниченной замкнутой области D на плоскости Xoy. Разобьем эту область произвольным образом на n частей Δ S1, Δ S2 … Δ Sn В каждой части Δ Si выберем произвольную точку Mi (ξ i; ρ i) и уменьшим значение функции в этой точке f(ξ i; ρ i) на площадь Δ Si. Сумма таких произведений новым частям области D
называется интегральной суммой. Обозначим DiamΔ Si диаметр Δ Si т.е. расстояние между наиболее удаленными точками этой части, maxdiam Δ Si - наибольший из диаметров всех частей данного разбиения. Определение: Двойным интегралом
Если такой предел существует, то функция f(x, y) называется интегрируемой в области D.
|
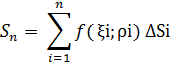
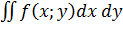от функции f(x, y) по области D называется предел интегральных сумм при условии maxdiamΔ Si→ 0, т.е. при неограниченном увеличении числа частей n независимо от выбора точек Мi
