Градиент
Пусть задана дифференцируемая функция Z=f(x, y). Геометрически она изображается поверхностью. Различные точки этой поверхности имеют различные аппликаты Z. Чтобы выделить на поверхности точки, находящиеся от плоскости на одном и том же расстоянии С, надо f(x, y)=С (геометрически провести секущую плоскость Z=C). Кривая в плоскости XOY, уравнение которой f(x, y)=С, называется линией уровня поверхности Z=f(x, y) т.е. линия уровня поверхности это множество всех точек плоскости, в которых данная функция принимает одно и то же значение. Если поверхность Z=f(x, y) пересечь плоскостями Z=C, где С – произвольная постоянная, и спроектировать полученные в сечениях линии на плоскость xOy, то на этой плоскости получиться семейство линий уровня f(x, y)=С с параметром С. Пример 1
Следовательно, линии уровня поверхности (эллипсоида) представляет собой семейство эллипсов с плоскостями a= 4
Пусть Z=f(x, y) определена в некоторой окрестности точки Мо(xo, yo) Определение. Градиентом функции Z=f(x, y) в точке Мо называется вектор, обозначаемый символом Градиент характеризует направление наискорейшего возрастания функции в заданной точке. Если рассматривать функцию трех переменных, в точке Мо(xo, yo zo) То Пример 2 С какой наибольшей скоростью моет возрастать функция
Наибольшая по абсолютной величине скорость изменения (возрастания или убывания) функции и при переходе точки М через точку Р численно равна модулю градиента функции в точке Р.
1). 2) Определение: Производной функции Z=f(x, y) в точке Мо(xo, yo) по направлению, определенному единичным вектором ē = cos α ī +cos β ĵ называется проекция
Соответственно, для функции U=f(x, y, z) производная в точке Мо(xo, yo, zo) по направлению вектора ē = cos α ī +cos β ĵ + cos p k имеет вид.
Пример3 Найти производную функцию u = xy+yz+1 по направлению вектора ē (12; -3; -4) в любой точке и в точках A(0; -2; -1) и B(3; 3; 5) Найдем частные производные функций и U направляющие косинусы вектора ē
Подставляя значения в формулу для Подставляя координаты точек А и В получим Задачи для самостоятельного решения: 1. С какой наибольшей скоростью может убывать функция U=ln (x2 - y2+z2) при переходе точки М(x, y, z) через точку М(1; 1; 1) 2. Найти градиент функции z=x2-y3-y ln x точке А(1; 2) 3. Для функции найдите модуль градиента в точке U=xy-y2+ez найдите модуль градиента в точке А(2; 2; 0) 4. Найдите производную функцию U=0, 5 z2 yy-x2—y arcsin (x-2) по направлению вектора ā = (1, 2, 2) в точке A(2, 4, 1); 5. Постройте линии уровня функции Z=x2+6x+y2, найдите ее производную по направлениям вектора
10. Кратные и криволинейные интегралы:
|
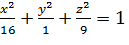Положим, что Z=C 
; 
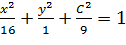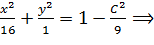
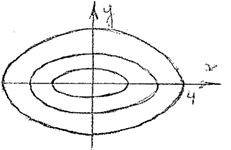
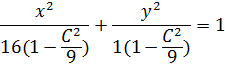
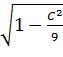; b= 
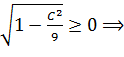
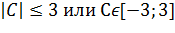
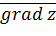и имеющий координаты равные соответственно производным 
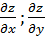вычисленным в точке Мо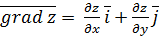 
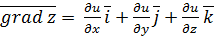
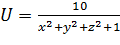при переходе точки М(x, y, z) через точку М(-1, 2, -1)? в каком направлении должна двигаться точка М при переходе черех точку М1(2; 0; 1), чтобы функция убывала с наибольшей скоростью?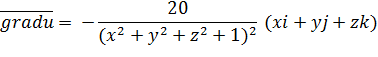 
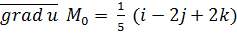его модуль, численно равный искомой наибольшей скорости вырастания функции и (М) при переходе через точку Мо будет 
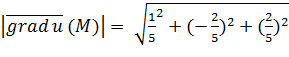= 3/5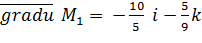
Искомый вектор имеющий прямо противоположное направление будет 
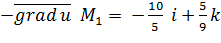Чтобы функция U убывала с наибольшей скоростью при переходе через точку М1 точка М должна двигаться в направлении вектора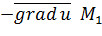 
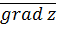на вектор ē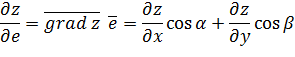
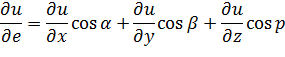
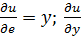= x+z; 
; 
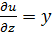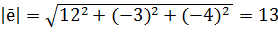
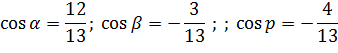
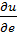получим 
8y-3(x+z)/13
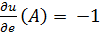
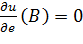
в точке K(-1; 1)
