Вычисление двойного интеграла
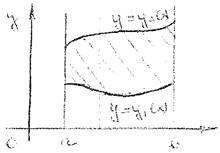
1. Если область интегрирования является правильной, т.е. D {(x; y): a≤ x≤ b, y1(x)≤ y≤ y2(x)}
2. Если D = {(x; y): c≤ y≤ d, x1(y)≤ x≤ x2(y)} т.е. с – наименьшее значение в области Д, d - наибольшее, x1(y) – уравнение левой границы области, x2(y) – уравнение правой границы, то двойной интеграл вычисляется сведением к повторному по формуле:
Если области D не является правильной, то ее разбивают на части, каждая з которых является правильной областью первого или второго вида. Для вычисления повторного интеграла, стоящего в правой части формулы (1), необходимо вычислить сначала внутренний определенный интеграл Переход от правой части формулы (1) к правой части формулы (2) или наоборот, называется изменением порядка интегрирования. Пример 1 Вычислить двойной интеграл
Сначала вычисляем внутренний интеграл по y, считая, что x=const
Затем вычисляем внешний интеграл
Следовательно
Пример 2. Изменить порядок интегрирования в повторном интеграле
(a
Центр этой окружности находится в точке с координатами (a; 0), радиус равен R=a линия При изменении порядка интегрирования область D разбивается линией y=a на три области D1; D2; D3. Линия y=a касательная к окружности в точке с координатами (a, a). Из уравнения параболы y2= Выразим x из уравнения окружности y=
Используя свойство адитивности двойного интеграла относительно отметки области интегрирования, получаем:
|




 по переменной y (x считается параметром) затем от полученного результата берется внешний интеграл по x. Аналогично для формулы (2) сначала вычисляется внутренний интеграл по переменной y (y считается параметром), затем x1(y) берется внешний интеграл по переменной y..
по переменной y (x считается параметром) затем от полученного результата берется внешний интеграл по x. Аналогично для формулы (2) сначала вычисляется внутренний интеграл по переменной y (y считается параметром), затем x1(y) берется внешний интеграл по переменной y.. dx dy по области D ограниченной линиями y=1/x; y=x; x=2;
dx dy по области D ограниченной линиями y=1/x; y=x; x=2;

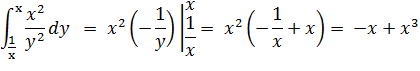


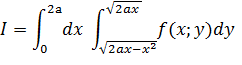



 , сверху – линией
, сверху – линией  а слева и справа прямыми x=0 и x=2a соответственно.
Линия y=
а слева и справа прямыми x=0 и x=2a соответственно.
Линия y=  расположенная над осью OX
расположенная над осью OX Следовательно, области D1; D2; D3.определяются неравенствами:
Следовательно, области D1; D2; D3.определяются неравенствами:




