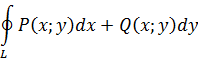Геометрические приложения двойного интеграла

 

Пример 1 Вычислить площадь фигуры, ограниченной параболами y²=10x+25, y²=-6x+9

Известно, что площадь плоской области D XOY вычисляется по формуле Построим область D. Парабола y2=10(x+2, 5) имеет величину в точке с координатами (-2, 5; 0). Ее ветви симметричны относительно оси Ox и направлена вправо.

Парабола y²=-6(x-1, 5) имеет вершину в точке с координатами (1, 5; 0). Ветви этой параболы симметричны относительно оси Ox и направлена влево. Решая систему уравнений, получим точки пересечения парабол:

Итак, область D можно представить в виде систем неравенств:

Таким образом, вычисляем площадь области Д

 

Пример 2 Вычислить площадь плоской фигуры, ограниченной линиями

(x²+ y²) ²= 2a² (x²-y²), y²+x²=a² (x²+ y²≥ a²)

Перейдем к полярным координатам a=ρ cosα, y=ρ sinα

Получим уравнения границы области в виде ρ =a (лемниската Бернулли) и ρ =a (окружность) при условии ρ ≥ a

Надо найти площадь плоской фигуры, ограниченной частью лемнискаты Бернулли ρ =a и частью окружности ρ =a летящей вне этой окружности. Найдем точки пересечения лемнискаты и окружности, решив систему уравнений:

 

⟹ 1= ⟹

Точка (a; π /6) является одной из четырех точек пересечения лемнискаты с окружностью. В силу симметрии области, искомая площадь равна четверти площади области, определяемой неравенствами:

Следовательно, площадь области можно найти по формуле:

 

Пример 3. Найти объем тела, ограниченного поверхностями,

x²+ y² = R²; (x²+z²) = R², (x≥ 0; y≥ 0; z≥ 0)

Объем V цилиндрического тела, ограниченного сверху поверхностью z=f(x; y) снизу плоскостью z=0 и боков – замкнутой цилиндрической поверхностью с образующими, параллельными оси Oz, вырезающей на плоскости Oxy область D, выражается интегралом: V=

Строим поверхности, ограничивающие тела: x2+ y2 = R2- круговой цилиндр у которого ось OZ является осью симметрии x2+ я2 = R2 – круговой цилиндр, у которого ось Oy является осью симметрии. На рисунке изображена часть этих цилиндров

 

Расположенные в первом октанте; область D является четвертью круга. Сверху тело ограничено x2+ y2 = R2 z≥ 0 поверхностью, откуда находим Следовательно, подынтегральная функция имеет вид f(x; y)= Вычисли объем тела:

V=

Задачи для самостоятельного решения:

Изменить порядок интегрирования:

1.

2. 3.

4.

Вычислить двойные интегралы

5. D – область, ограниченная линиями xy=1, y= x=2

6. D– область, ограниченная линиями xy=4, x+y=5

7. D– область, ограниченная линиями y=e^x, x =0, y=2

Используя полярные координаты. Найти площадь фигур, ограниченных линиями.

8. x²+y²=2ax, x²+y²=2bx, y=x, y=0 (0< a< b)

9. (x²+y²)²= 2a²xy (a> 0) Найти объемы тел, ограниченных поверхностями:

10. z=0, y=x, x=0

11. Z = 2-x-y, z=0, x²+y²=1, x=0, x=0, y=0

12. Z= x²+y², z=0, y²=x, x=1

 

10.4. Криволинейный интеграл второго типа:

Пусть функции P(x, y), Q(x, y) являются непрерывными вдоль дуги L, расположенной в плоскости XOY. Разобьем дугу L на участков в каждом таком участке выберем по произвольной точкеA_k (ξ _k; η _k). Обозначим проекции k- го участка на оси координат через Δ x_k, Δ y_k и составим сумму

Эта сумма называется n–ой интегральной суммой по линии L, а ее предел при стремлении к нулю длины наибольшего частичного участка разбиения кривой L, называется криволинейным интегралом второго типа по дуге L.

Дуга L называется линией или контуром интегрирования

В частности, если Q(x; y)=0 то криволинейный интеграл имеет вид и называется криволинейным интегралом по координате x Если P(x; y)=0 то называется криволинейным интегралом по координате y.

Определение криволинейного интеграла остается в силе и в том случае, когда кривая L замкнута. Для обозначения криволинейного интеграла по замкнутому контуру часто употребляется символ:

с обязательным указанием направления обхода. В случаях, когда криволинейных интеграл от векторной функции f{P; Q} берется по замкнутой кривой, то этот криволинейный интеграл называется циркулярным вектора F по замкнутому контуру L