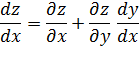Производная сложной функции. Полная производная
Пусть в уравнении Z=f(u, v) переменные u, v являются функциями независимых переменных x и y u=φ (x, y), v= φ (x, y), тогда Z есть сложная функция от x и y.
т.е. производная сложно заданной функции по независимой переменной равна сумме произведений частных производных по промежуточным переменным на частичные производные этих переменных по независимой переменной. Пример. Z= arc Tg u/v, где u=x Sin y, v=y Sin x,
Пример: Z= x/y
|








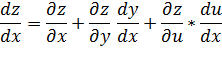
 найти
найти