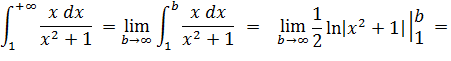Несобственные интегралы. с бесконечными пределами (1-го порядка)с бесконечными пределами (1-го порядка) Пусть функция f(x) определена и непрерывна при всех a ≤ x≤
Если существует конечный предел
В этом случае говорят, что несобственный интеграл Аналогично определяется и следующие несобственные интегралы:
где с – любое число
Если пределы в правой части этих формул существуют и конечные, то несобственные интегралы – сходящиеся, в противном случае – расходящиеся. Пример 1.
Интеграл сходится Пример 2.
Интеграл расходится
|
рассмотрим
Он имеет смысл при любом b> a. При изменении b он является функцией от b. Пусть b → + 
то этот предел называют несобственным интегралом от функции f(x) на [a, +œ ] и обозначают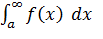
, так что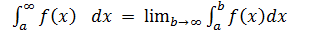 
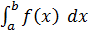при b → + 
