Интегрирование тригонометрических функций
1) Интегралы вида Sin mx cos nx = ½ (sin (m-n)x + sin (m+n)x); Cos mx cos nx = ½ (cos (m-n)x + cos (m+n)x); Sin mx cos nx =½ (cos (m-n)x - cos (m+n)x); Например
= -1/4 cos 2x – 1/20 cos 10x+C 2) Интегралы вида
1) 2) Если под знаком интеграла вида
3. 4. 7.6. Интегрирование некоторых ирракционных функций Интервалом вида
Где В результате подстановки каждая дробная степень x выразится через целую степень t и, следовательно, подынтегральная функция преобразится в рациональную функцию оси t. 1. = =6( 2. = -4
|

 берутся с помощью формул:
берутся с помощью формул:
 где два показателя степени n и m- четные числа или 0, требуют исполнения формул понижения степени:
где два показателя степени n и m- четные числа или 0, требуют исполнения формул понижения степени:
 = ¼
= ¼  1/4x +1/12Sin6x+1/8(
1/4x +1/12Sin6x+1/8(

 dx =
dx = 
 хотя бы один из показателей степени m и n число нечетное, то от нечетной степени функции (sinx или cosx) отделяют первую степень, а оставшуюся четную степень функции заменяют на кофункцию по формуле
хотя бы один из показателей степени m и n число нечетное, то от нечетной степени функции (sinx или cosx) отделяют первую степень, а оставшуюся четную степень функции заменяют на кофункцию по формуле  или
или 


 вычисляются с помощью подстановки
вычисляются с помощью подстановки


 - общий знаменатель дроби
- общий знаменатель дроби =
=  =
=  =
=  = 6
= 6  =
= -
-  =
=  =
=  =
= =
=  = 2
= 2 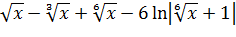 +C;
+C; =
= 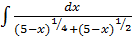 =
=  =
=  =
= =
=  dt = -4(
dt = -4( ) = -4 (
) = -4 ( ) = - 4 (
) = - 4 ( -2
-2 



