Функция y=f(x) называется возрастающей (убывающей) в интервале (а, в), если для любых  и
и 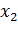 , принадлежащих интервалу, из неравенства
, принадлежащих интервалу, из неравенства 
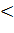
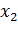 следует неравенство f(
следует неравенство f(  )
) 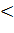 f(
f(  ). f(
). f(  )
) 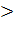 f(
f( 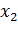 ).
).
Если функция y=f(x) дифференцируема в интервале (а, в) и f'(x) 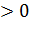 при всех
при всех
x €(а, в), то функция y=f(x) возрастает в этом интервале, если же f'(x) 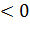 для всех x €(а, в), то f(x) в этом интервале убывает.
для всех x €(а, в), то f(x) в этом интервале убывает.
Точка  называется точкой максимума (минимума) функции f(x), если существует окрестность точки
называется точкой максимума (минимума) функции f(x), если существует окрестность точки  , для всякой точки
, для всякой точки  которой выполняется неравенство f(
которой выполняется неравенство f(  )
) 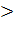 f(
f( 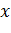 ) (f(
) (f(  )
) 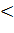 f(
f( 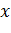 )). Максимум и минимум функции объединяются общим названием – экстремум функции.
)). Максимум и минимум функции объединяются общим названием – экстремум функции.
Необходимое условие экстремума. Если  – точка экстремума дифференцируемой функции y=f(x), то f'(
– точка экстремума дифференцируемой функции y=f(x), то f'(  )
) 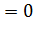
Отсюда следует, что точки, в которых функция имеет экстремум, следует искать среди тех внутренних точек ее области определения, где либо f'(  )
) 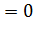 , либо f'(
, либо f'( 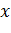 )
) 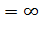 , либо f'(
, либо f'( 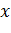 ) не существует. Такие точки называются критическими.
) не существует. Такие точки называются критическими.
Достаточное условие экстремума. Если при переходе через критическую точку  слева направо производная функции y=f(x) меняет знак с плюса на минус (с минуса на плюс), то
слева направо производная функции y=f(x) меняет знак с плюса на минус (с минуса на плюс), то  является точкой максимума (минимума) функции y=f(x). Если же производная f'(
является точкой максимума (минимума) функции y=f(x). Если же производная f'( 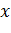 ) знака не меняет, то в точке
) знака не меняет, то в точке  экстремума нет.
экстремума нет.
Пример. Найти интервалы возрастания и убывания и экстремумы функции
f(x) = x + 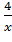 .
.
Решение.
Область определения функции: 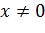 , т.е. (-
, т.е. (- 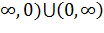 . Находим производную:
. Находим производную:
f'( 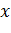 )=
)= 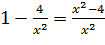
Приравниваем ее к нулю и находим критические точки:
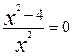 при
при 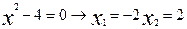 и не существует при
и не существует при  , но в точке
, но в точке  функция не определена, следовательно экстремума в этой точке быть не может.
функция не определена, следовательно экстремума в этой точке быть не может.

Следовательно, функция возрастает в интервалах 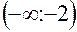 и
и 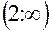 и убывает в интервалах
и убывает в интервалах  и
и 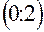 . В точке
. В точке 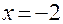 возрастание сменяется на убывание, следовательно, это точка максимума и
возрастание сменяется на убывание, следовательно, это точка максимума и  - точка максимума. В точке
- точка максимума. В точке  убывание функции сменяется на возрастание, следовательно это точка минимума и
убывание функции сменяется на возрастание, следовательно это точка минимума и
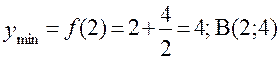 - точка минимума.
- точка минимума.


 и
и 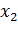 , принадлежащих интервалу, из неравенства
, принадлежащих интервалу, из неравенства 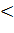
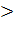 f(
f( 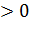 при всех
при всех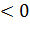 для всех x €(а, в), то f(x) в этом интервале убывает.
для всех x €(а, в), то f(x) в этом интервале убывает. называется точкой максимума (минимума) функции f(x), если существует окрестность точки
называется точкой максимума (минимума) функции f(x), если существует окрестность точки  которой выполняется неравенство f(
которой выполняется неравенство f( 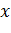 ) (f(
) (f( 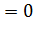
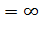 , либо f'(
, либо f'(  слева направо производная функции y=f(x) меняет знак с плюса на минус (с минуса на плюс), то
слева направо производная функции y=f(x) меняет знак с плюса на минус (с минуса на плюс), то 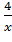 .
.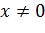 , т.е. (-
, т.е. (- 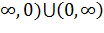 . Находим производную:
. Находим производную: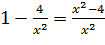
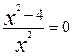 при
при 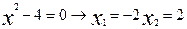 и не существует при
и не существует при  , но в точке
, но в точке 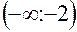 и
и 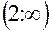 и убывает в интервалах
и убывает в интервалах  и
и 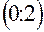 . В точке
. В точке 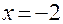 возрастание сменяется на убывание, следовательно, это точка максимума и
возрастание сменяется на убывание, следовательно, это точка максимума и  - точка максимума. В точке
- точка максимума. В точке  убывание функции сменяется на возрастание, следовательно это точка минимума и
убывание функции сменяется на возрастание, следовательно это точка минимума и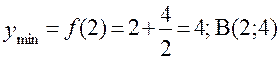 - точка минимума.
- точка минимума.


