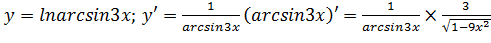Основные правила дифференцирования.
Пусть и = и(x), V=V(x) – дифференцируемые функции, c – const. Имеют место формулы: 1) 6) Производная сложной функции. Пусть функциональная зависимость y от x задана следующим образом:
Производная сложной функции равна произведению производной данной функции по промежуточному аргументу и на производную промежуточного аргумента по x. Основные формулы дифференцирования. 1) 2) 3) 4) 5) 6) 7) 8) 11) 13) Например. Вычислить производные: 1) 2) 3) 4) 5) 6) 7) 8) 9) 10)
|
; 4) 
; 5) 
, где u= 
(т.е. 
сложная функция) и в некоторой точке x функция u= 
, а функция 
. Тогда сложная функция 
в точке x также имеет производную, которая равна 
или коротко:
', т.е.
(α -const)
(частный случай (1) при α = 
)
(a – const, a 
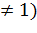
(частный случай (3) при a = e)
= 
(a – const, a 
(частный случай (5) при a = e)
10) 
;
14)) 
= 
; 
= 
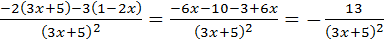
sin 
; 
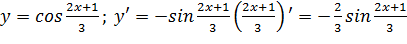
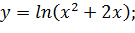
