6.1. Определение производной.
Пусть задана функция y=f(x), определенная в некотором промежутке и пусть x – некоторая точка этого промежутка, в котором значение функции равно
y=f(x). Пусть аргумент x получил некоторое приращение  . Новое (наращенное) значение аргумента
. Новое (наращенное) значение аргумента  , ему соответствует наращенное зачение функции
, ему соответствует наращенное зачение функции  , т.е. функция получила приращение
, т.е. функция получила приращение  . Составим отношение приращения функции к приращению аргумента:
. Составим отношение приращения функции к приращению аргумента:

Определение. Производной функции y=f(x) по аргументу x называется предел отношения приращения функции  к вызываемому его приращение аргумента
к вызываемому его приращение аргумента  , когда
, когда  произвольным образом стремиться к нулю.
произвольным образом стремиться к нулю.
Обозначения для производной:  ;
;  ;
;  так что
так что

Значение производной в точке  обозначается:
обозначается:
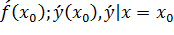
Операция нахождения производной от функции  называется дифференцированием этой функции:
называется дифференцированием этой функции:
 Геометрический смысл производной
Геометрический смысл производной
Пусть в плоскости Oxy задана кривая y=f(x) и точка  , принадлежащая этой кривой, имеет абсциссу
, принадлежащая этой кривой, имеет абсциссу  .
.
Производная  , вычисленная в точке касания, равна угловому коэффициенту касательной, проведенной к графику функции y=f(x) в точке
, вычисленная в точке касания, равна угловому коэффициенту касательной, проведенной к графику функции y=f(x) в точке 
 , где
, где  - угол, образованный касательной с положительным направлением оси Ox.
- угол, образованный касательной с положительным направлением оси Ox.
 Геометрический смысл производной
Геометрический смысл производной

 . Новое (наращенное) значение аргумента
. Новое (наращенное) значение аргумента  , ему соответствует наращенное зачение функции
, ему соответствует наращенное зачение функции  , т.е. функция получила приращение
, т.е. функция получила приращение  . Составим отношение приращения функции к приращению аргумента:
. Составим отношение приращения функции к приращению аргумента:
 к вызываемому его приращение аргумента
к вызываемому его приращение аргумента  ;
;  ;
;  так что
так что
 обозначается:
обозначается: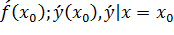
 называется дифференцированием этой функции:
называется дифференцированием этой функции:
 , принадлежащая этой кривой, имеет абсциссу
, принадлежащая этой кривой, имеет абсциссу  .
. , вычисленная в точке касания, равна угловому коэффициенту касательной, проведенной к графику функции y=f(x) в точке
, вычисленная в точке касания, равна угловому коэффициенту касательной, проведенной к графику функции y=f(x) в точке  , где
, где  - угол, образованный касательной с положительным направлением оси Ox.
- угол, образованный касательной с положительным направлением оси Ox.


