Прямая на плоскости
Пусть l – производная прямая на плоскости b прямоугольной декартовой системе координат Oxy. Любой вектор 1) 2) A 3) 4) 5) 6) y = kx + b, где k – угловой коэффициент, b – величина отрезка, отсекаемого прямой на оси Oy Если заданы две прямые уравнениями
Условие параллельности двух прямых: Условие перпендикулярности двух прямых: Если прямые заданы уравнениями с угловым коэффициентом: Tg y = Условие параллельности двух прямых:
Условие перпендикулярности двух прямых:
Задача 1. Найти угловой коэффициент прямой, заданной общим уравнением Решение. Выразим из этого уравнения y:
Задача 2. Найти точку А пересечения прямых
Решение. Так как искомая точка лежит на каждой из двух прямых, то координаты этой точки удовлетворяют каждому из уравнений. Поэтому координаты точки пересечения прямых находятся из системы уравнений.
Задача 3. Составить уравнение прямой по следующим данным: 1) прямая проходит через точку М (2; - 3) под углом 2) прямая проходит через точку М (2; - 3) параллельно прямой 3) прямая проходит через точку М (2; - 3) перпендикулярно прямой 4) прямая проходит через точку М (2; - 3) перпендикулярно вектору 5) прямая проходит через точку М (2; - 3) и через точку X (4; 1) Решение. 1) Поскольку прямая образует с осью OX угол
2) Прямая
Поскольку искомая прямая
3) Поскольку искомая прямая 4) Вектор 5) Известны две точки, через которые проходит прямая, поэтому используем уравнение (4):
или Задачи для самостоятельного решения. 1) Какой угловой коэффициент имеет прямая, проходящая через точки А(4; 2) и В(-1; 3)? 2) Составить уравнение перпендикуляра, опущенного из точки А(3; 2) на прямую, проходящую через точки В(5; 3) и С(-2; 1) 3) Составить уравнение прямой, проходящей через точку А(1; -3) и точку пересечения прямых
|


 , параллельный прямой l, называется направляющим вектором прямой, а вектор
, параллельный прямой l, называется направляющим вектором прямой, а вектор  , перпендикулярный к прямой l, называется вектором нормали. Прямая может быть задана уравнением одного из следующих видов:
, перпендикулярный к прямой l, называется вектором нормали. Прямая может быть задана уравнением одного из следующих видов: - общее уравнение прямой, коэффициенты А и В являются координатами вектора нормали.
- общее уравнение прямой, коэффициенты А и В являются координатами вектора нормали. - уравнение прямой, проходящей через точку
- уравнение прямой, проходящей через точку  с вектором нормали
с вектором нормали 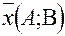 .
. – уравнение прямой, проходящей через точку
– уравнение прямой, проходящей через точку  с направляющим вектором
с направляющим вектором  - уравнение прямой, проходящей через две заданные точки
- уравнение прямой, проходящей через две заданные точки  и
и 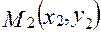
 - уравнение прямой, проходящей через точку
- уравнение прямой, проходящей через точку 
 , то угол между этими прямыми находится как угол между их векторами нормалей
, то угол между этими прямыми находится как угол между их векторами нормалей  :
: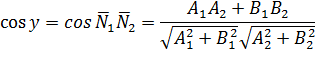


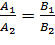
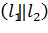



 , то угол y между прямыми находится по формуле:
, то угол y между прямыми находится по формуле: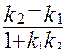



 и
и 
 и
и 


 к оси OX
к оси OX

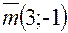
 . Используем формулу (5):
. Используем формулу (5):


 параллельна прямой
параллельна прямой  , то вектор
, то вектор  будет вектором нормали и к прямой
будет вектором нормали и к прямой 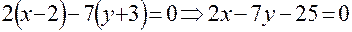
 перпендикулярна к заданной прямой
перпендикулярна к заданной прямой  будет ей параллелен, т.е. будет для нее направляющим вектором. Используем формулу (3):
будет ей параллелен, т.е. будет для нее направляющим вектором. Используем формулу (3): 
 , перпендикулярный прямой, будет для нее вектором нормали, поэтому по формуле (2) имеем:
, перпендикулярный прямой, будет для нее вектором нормали, поэтому по формуле (2) имеем: 


 и
и  перпендикулярно прямой
перпендикулярно прямой 



