Векторным произведением вектора  на вектор
на вектор  называется вектор
называется вектор  , обозначаемый символом
, обозначаемый символом 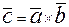
 или
или  и определяемый условиями:
и определяемый условиями:

1) 1) вектор  перпендикулярен своим перемножаемым векторам:
перпендикулярен своим перемножаемым векторам:  и
и  , следовательно перпендикулярен к плоскости этих векторов
, следовательно перпендикулярен к плоскости этих векторов
2) Тройка векторов  и
и  - правая, т.е. если смотреть с конца вектора
- правая, т.е. если смотреть с конца вектора  , то кратчайший поворот от вектора
, то кратчайший поворот от вектора  к вектору
к вектору  осуществляется против часовой стрелки;
осуществляется против часовой стрелки;
3) 
 .
.
Геометрический смысл векторного произведения:  = S параллелограмма, т.е. модуль векторного произведения
= S параллелограмма, т.е. модуль векторного произведения  численно равен площади параллелограмма, построенного на векторах
численно равен площади параллелограмма, построенного на векторах  и
и  :
:
Иначе, площадь параллелограмма, построенного на векторах  и
и  , численно равна модулю векторного произведения векторов
, численно равна модулю векторного произведения векторов  и
и  :
:
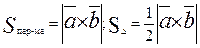
Свойства векторного произведения:
1) 
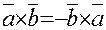
2) 
3) 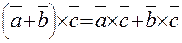
4) 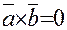 , если ненулевые векторы коллинеарны.
, если ненулевые векторы коллинеарны.
Если векторы  и
и  заданы координатами:
заданы координатами:
 , то векторное произведение
, то векторное произведение  x
x  вычисляется по формуле:
вычисляется по формуле:

Например, если  , то
, то


Задача 1. Заданы координаты вершин треугольника АВС: А(1; -1; 0), В(3; 1; 1), С(-1; 0; 2). Найти его площадь.

Решение.



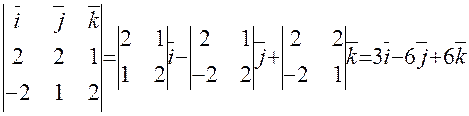
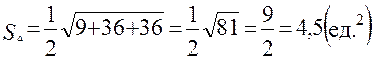
Задача 2.Найти длину опущенной на вектор  высоты параллелограмма, построенного на векторах
высоты параллелограмма, построенного на векторах 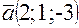 и
и 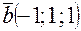 .
.
Решение.


 , с другой стороны
, с другой стороны


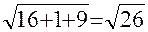
 . Подставляя в формулу, получаем
. Подставляя в формулу, получаем

Задачи для самостоятельного решения:
1) Найти 
2) Векторы  и
и  являются сторонами параллелограмма. Найти площадь параллелограмма, построенного на его диагоналях.
являются сторонами параллелограмма. Найти площадь параллелограмма, построенного на его диагоналях.
3) Найти длину опущенной на сторону АС высоты треугольника АВС, если А(2; -1; -1), В(1; 1; 2), С(-1; -1; 3).
 Решение.
Решение.


 на вектор
на вектор  называется вектор
называется вектор  , обозначаемый символом
, обозначаемый символом 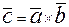
 или
или  и определяемый условиями:
и определяемый условиями:
 перпендикулярен своим перемножаемым векторам:
перпендикулярен своим перемножаемым векторам:  и
и  , следовательно перпендикулярен к плоскости этих векторов
, следовательно перпендикулярен к плоскости этих векторов и
и  - правая, т.е. если смотреть с конца вектора
- правая, т.е. если смотреть с конца вектора  .
. численно равен площади параллелограмма, построенного на векторах
численно равен площади параллелограмма, построенного на векторах  и
и 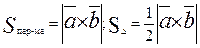
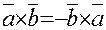

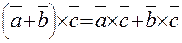
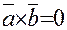 , если ненулевые векторы коллинеарны.
, если ненулевые векторы коллинеарны. , то векторное произведение
, то векторное произведение 
 , то
, то



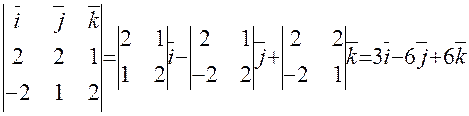
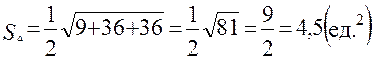
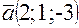 и
и 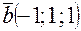 .
. , с другой стороны
, с другой стороны

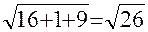
 . Подставляя в формулу, получаем
. Подставляя в формулу, получаем

 и
и  являются сторонами параллелограмма. Найти площадь параллелограмма, построенного на его диагоналях.
являются сторонами параллелограмма. Найти площадь параллелограмма, построенного на его диагоналях.


