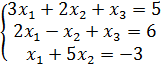Задачи для самостоятельного решения. Для данных матриц найти обратные:
Для данных матриц найти обратные: 1)
A = Пример. Решить матричным методом систему уравнений:
Решение. Вводим обозначения: A = Тогда система может быть записана в матричной форме AX=B и ее решение имеет вид
Ищем матрицу
C = Находим решение матричного уравнения:
3)
Векторная алгебра.
|
; 2) 
; 3) 
. Решение систем линейных уравнений матричным методом:
адана система линейных уравнений:
сли ввести обозначения: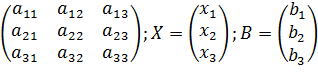
, то систему уравнений можно записать в матричной форме: A 
. Умножив это уравнение на 
слева, получаем 
- решение системы в матричной форме.
; 
, следовательно, 
= 1;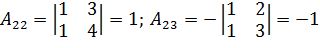 
– решение системы.
ить матричным методом системы уравнений:
2) 
