Определители. 359. Шопенгауэр А. Эристика, или Искусство побеждать в спорах
359. Шопенгауэр А. Эристика, или Искусство побеждать в спорах. - СПб.: 1900.
КРАТКИЙ КОНСПЕКТ ЛЕКЦИЙ ПО ВЫСШЕЙ МАТЕМАТИКЕ
Ростов-на-Дону Составитель: Л.В. Сахарова УДК 517 С 221
Настоящее пособие соответствует программе курса высшей математики технических учебных заведений и содержит краткий конспект лекций по темам «Определители», «Линейная алгебра», «Аналитическая геометрия», «Пределы», «Дифференциальное исчисление функции одной переменной», «Неопределенный интеграл», «Определенный интеграл», «Функции нескольких переменных», «Кратные и криволинейные интегралы». Используемые символика и терминология соответствуют учебным пособиям, рекомендуемым программой курса высшей математики.
Определители 1.1. Определители второго порядка. Пусть дана квадратная таблица из четырех чисел Определителем второго порядка называют число, обозначаемое символом
Элементы Пример 1. Вычислить Решение.
Пример 2. Решить уравнение Решение.
Пример 3. Решить неравенство Решение.
3x < - 9; x < - 3 Примеры для самостоятельного решения. Вычислить определители: 1). Решить уравнения. 1) Решить неравенства. 1) 1.2. Определители третьего порядка. Пусть задана квадратная таблица из девяти чисел:
Определителем третьего порядка, соответствующим этой таблице, называется число, обозначаемое символом
Пример 1. Вычислить Решение.
Пример 2. Решить уравнение: Решение.
25 – 4 x – 6 – 10 x – 60 – 1 = 0 => - 14 x – 42 = 0; 14 x = – 42; x = - 3. Пример 3. Решить неравенство: Решение.
-3 x + 2 – 4 + x + 12 – 2 < 1; - 2 x + 8 < 1; 2 x > 7; x > Решить самостоятельно: Вычислить определители: 1). Решить уравнения: 1). Решить неравенство:
1.2. Решение систем трех-линейных уравнений с тремя неизвестными методом Крамера. Рассмотрим систему уравнений:
Введем обозначения: ∆ = Имеет место теорема: Если определитель системы ∆ ≠ 0, то система имеет единственное правильное решение, которое может быть получено по формулам Крамера: x = Пример. Решить систему уравнений:
Решение. ∆ = x=
Решить системы уравнений: 1).
|


 :
: 
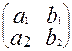
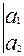
 и вычисляемое по правилу:
и вычисляемое по правилу:
 и
и  лежат на главной диагонали, а элементы
лежат на главной диагонали, а элементы  и
и  – на побочной диагонали. Следовательно, чтобы вычислить определитель, надо из произведения чисел, стоящих на главной диагонали, вычесть произведение чисел, стоящих на побочной диагонали.
– на побочной диагонали. Следовательно, чтобы вычислить определитель, надо из произведения чисел, стоящих на главной диагонали, вычесть произведение чисел, стоящих на побочной диагонали.

 2 - 4
2 - 4  = 6 + 20 = 26
= 6 + 20 = 26
 = 0
= 0

 > 5
> 5
 ; 2).
; 2). 
 ; 3).
; 3). 


 = 0; 2)
= 0; 2) 
 =0; 3)
=0; 3) 
 = 0
= 0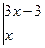
 > 0; 2)
> 0; 2) 
 < 0; 3)
< 0; 3) 
 > 10
> 10
 и вычисляемое по правилу:
и вычисляемое по правилу:





 = 0
= 0

 < 1
< 1


 ; 2).
; 2). 

 ; 3)
; 3) 

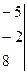

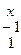
 = 0; 2).
= 0; 2). 

 = 0
= 0

 > 0
> 0 с неизвестными
с неизвестными  ; ∆ y =
; ∆ y =  ; ∆ z =
; ∆ z = 
 ; y =
; y =  ; z =
; z = 
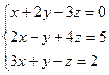

 = 10; ∆ x =
= 10; ∆ x = 


 = 15;
= 15; =
=  ; y =
; y = 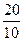 = 2; z =
= 2; z =  =
= 
 2).
2).  3).
3). 



