Свойства координат векторов
1) Равные векторы имеют равные координаты, т.е. если 2) При сложении (вычитании) векторов их соответственные координаты складываются (вычитаются), т.е. если 3) При умножении вектора на число каждая его координата умножается на это число, т.е. если 4) Координаты коллинеарных векторов пропорциональны, т.е. если Простейшие задачи: 1) Модуль (длина) вектора 2) Если вектор 3) Если заданы координаты точек А
Задача 1. Векторы
|
(
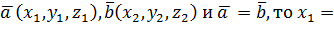
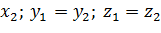
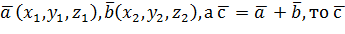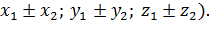
, а 
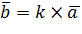, то 
(kx; ky; kz)
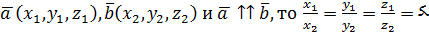
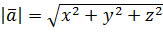
задан координатами начальной и конечной точек (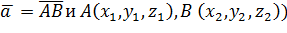
, то для получения куоординат вектора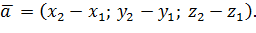 
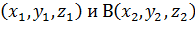, а точка С – середина отрезка АВ, то координаты точки С определяются по формулам:
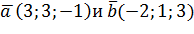являются сторонами параллелограмма. Найти длины его диагоналей.
