Линейные операции над матрицами
К линейным операциям относятся операция сложения матриц и умножение матрицы на число. Матрицы одинакового размера можно сложить, при этом получается матрица того же размера: Пусть A = Например: Любую матрицу можно умножить на любое число, при этом на это число умножается каждый элемент матрицы, т.е. если A = Например: A = B = Пример. Дано: A = Решение. С = 2 2.3. Умножение матриц. Перемножение матриц возможно лишь в том случае, когда число столбцов первого множителя равно числу сток второго множителя. В противном случае умножение невозможно. Пусть даны матрицы: A = При умножении матрицы A размера m x n на матрицу B размера n x p получается матрица C размера m x p. Элемент Cij этой матрицы равен сумме произведений элементов i-ой строки матрицы A на соответствующие элементы j-ого столбца матрицы B, т.е.
Пример 1. Дано: A = Решение.
 B = B =       = = 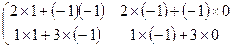 
= Пример 2. Найти f (A), если A = Решение. f (A)= Задачи для самостоятельного решения. Вычислить: 1) 4)A = 5)A =
Пусть задана квадратная матрица A. Матрицей, обратной к матрице А, называется такая квадратная матрица Пусть задана квадратная матрица третьего порядка: A= Обратная матрица определяется формулой:
Чтобы найти 1) Вычислить 2) Вычислить алгебраические дополнения элементов матрицы А; 3) Составить матрицу С, заменив все элементы матрицы А их алгебраическими дополнениями, транспонировав полученную матрицу; 4) Найти обратную матрицу: Пример. Найти обратную матрицу A = Решение. 1) 2)
3) C = 4) Проверка: A
|


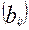 размера m x n, а C = A+B, тогда
размера m x n, а C = A+B, тогда  = a ij + b ij, i = 1, 2
= a ij + b ij, i = 1, 2  m; j = 1, 2,
m; j = 1, 2, 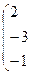
 ; B =
; B = 
 , а C = A+B. Тогда C =
, а C = A+B. Тогда C = 
 =
= 

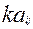 ) mn.
) mn.
 , а B = 3A, тогда
, а B = 3A, тогда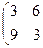


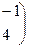 , а B =
, а B = 
 . Найти C = 2A – 3B.
. Найти C = 2A – 3B.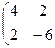
 +
+ 
 =
= 
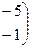 .
.
 и B =
и B = 

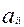
 +
+ 
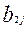 + …+
+ …+ 
 =
= 
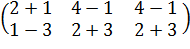 =
= 
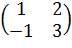 ; f (x) =
; f (x) = 
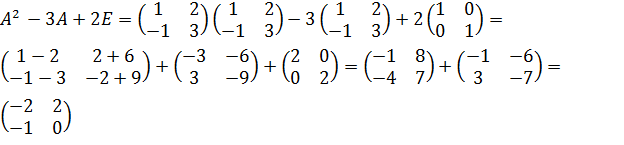 .
. ; 2)
; 2)  ; 3)
; 3) 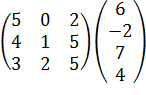
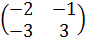 ; f (x) =
; f (x) =  Найти f (A).
Найти f (A). ; f (x) =
; f (x) =  . Найти f (A).
. Найти f (A). 4. Обратная матрица.
4. Обратная матрица. . Пусть дан определитель
. Пусть дан определитель  . Минором некоторого элемента называется определитель, получаемый из данного путем вычеркивания строки и столбца, на пересечении которых расположен данный элемент. Алгебраическое дополнение любого элемента определяется равно его минору, взятому со своим знаком, если сумма номеров строки и столбца, на пересечении которых расположен элемент, есть число четное и с обратным знаком, если это число нечетное. Например, алгебраическое дополнение элемента
. Минором некоторого элемента называется определитель, получаемый из данного путем вычеркивания строки и столбца, на пересечении которых расположен данный элемент. Алгебраическое дополнение любого элемента определяется равно его минору, взятому со своим знаком, если сумма номеров строки и столбца, на пересечении которых расположен элемент, есть число четное и с обратным знаком, если это число нечетное. Например, алгебраическое дополнение элемента  равно:
равно: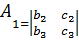 . Для элемента
. Для элемента  = -
= -  ,
, 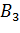 = -
= -  и т.д.
и т.д. , что A
, что A  =
=  . Матрица A имеет обратную только в том случае, если ее детерминант отличен от нуля:
. Матрица A имеет обратную только в том случае, если ее детерминант отличен от нуля:  .
. или иначе A=
или иначе A= 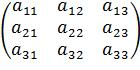
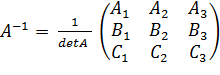 =
=  или
или 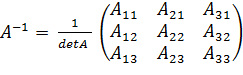 .
. , если
, если  , то обратная матрица существует;
, то обратная матрица существует;
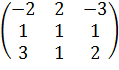


 = - 7;
= - 7; 
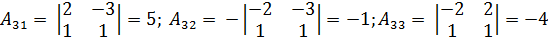


 .
.


