Скалярное произведение векторов
Скалярным произведением двух векторов
Поскольку Свойства скалярного произведения: 1) 2) 3) 4) Скалярное произведение двух ненулевых векторов равно нулю тогда и только тогда, когда эти векторы взаимно перпендикулярны:
Из формул (1) и (2) получаются формулы, наиболее часто используемые при решении задач: Cos Пусть векторы
Cos (
Задача 1. Найти Решение.
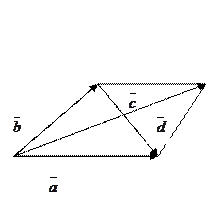
Задача 2. Найти угол между диагоналями параллелограмма, построенного на векторах
Требуется найти угол между векторами
Cos( Следовательно ( Задача 3. При каком значении l векторы Решение. Векторы
Задача 4. Даны координаты вершин треугольника АВС: А(-3; 4; 1), В(0; 4; -2), С(1; 2; 2). Найти Решение. Обозначим через
Задачи для самостоятельного решения. 1) Даны векторы 2) Даны координаты вершин треугольника АВС: А(2; 2; 4), В(3; 1; 0), С(1; 0; 2). Найти углы треугольника и 3) Даны последовательные вершины 4-угольника: А(3; α; -1), В(2; 1; α), С(2α; -3; -1). При каком α его диагонали взаимно перпендикулярны?
|

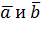 называется число, равное произведению модулей этих векторов на косинус угла между ними:
называется число, равное произведению модулей этих векторов на косинус угла между ними: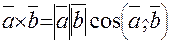 (1)
(1)
 , то
, то 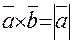
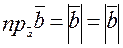
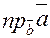 (2)
(2)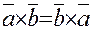

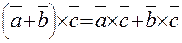
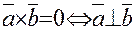 (3)
(3) ; (4);
; (4); 
 (5).
(5). . Тогда
. Тогда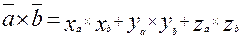
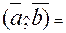
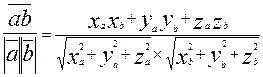
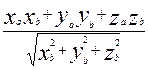
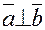 , если
, если 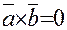 , т.е.
, т.е. 
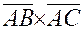 , если А (3; 2; -1), В (-1; 1; 2), С(5; 3; -3).
, если А (3; 2; -1), В (-1; 1; 2), С(5; 3; -3).
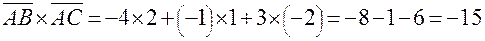
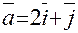 и
и  .
. Решение.
Решение.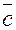 и
и 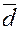 .
.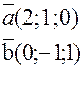
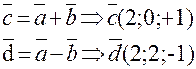
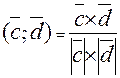
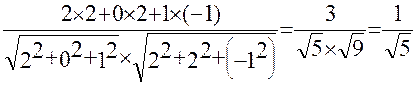
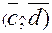 = arccos
= arccos 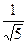 .
.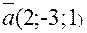 и
и 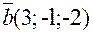 взаимно перпендикулярны?
взаимно перпендикулярны?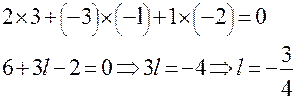
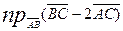
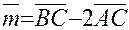 и найдем координаты этого вектора:
и найдем координаты этого вектора:
 и
и 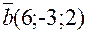 . Найти
. Найти 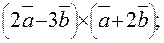

 .
.


