Векторы и линейные операции над ними
Вектором Вектор, у которого начало совпадает с концом, называется нуль-вектором. Векторы, которые расположены на одной или на параллельных прямых, называются коллинеарными. Векторы, которые параллельны некоторой плоскости, называются компланарными. Два вектора равны Произведением вектора 1) 2) 3) если λ > 0, то
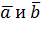 можно двумя способами: по правилу треугольника, пристроив их один к другому (Рис.1) и по правилу параллелограмма, отнеся векторы к общему началу (Рис.2). Если на векторах можно двумя способами: по правилу треугольника, пристроив их один к другому (Рис.1) и по правилу параллелограмма, отнеся векторы к общему началу (Рис.2). Если на векторах 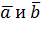 построен параллелограмм, то диагональ, исходящая из общего начала векторов, будет суммой этих векторов, а вторая диагональ – их разностью. построен параллелограмм, то диагональ, исходящая из общего начала векторов, будет суммой этих векторов, а вторая диагональ – их разностью.
       Рис.1 Рис.1  Рис.2 Рис.2

Рассмотрим прямоугольную систему координат Oxyz. На каждой оси выберем opm (единичный вектор). Три единичных вектора
(рис.3).
Произвольный вектор
Равенство (1) называется разложением вектора
|

 называется направленный отрезок, точка А – начало вектора, точка В – конец.
называется направленный отрезок, точка А – начало вектора, точка В – конец. , если 1) они коллинеарны, 2) одинаково направлены (
, если 1) они коллинеарны, 2) одинаково направлены ( и 3) их длины (модули) равны:
и 3) их длины (модули) равны:  .
. , определяемый следующими условиями:
, определяемый следующими условиями:
 и
и  коллинеарны (
коллинеарны (






 называются декартовым прямоугольным (ортнормированным) базисом в пространстве
называются декартовым прямоугольным (ортнормированным) базисом в пространстве
 , где (1) x =
, где (1) x =  , y =
, y =  z =
z = 
 , а числа x y z называют координатами вектора
, а числа x y z называют координатами вектора  .
.


