Свойства смешанного произведения
1) Смешанное произведение не меняется при круговой перестановке cомножителей, т.е. 2) Смешанное произведение меняет знак при перестановке любых двух сомножителей, например
Геометрический смысл смешанного произведения: модуль смешанного произведения некомпланарных векторов
Если Если векторы заданы координатами:
Например, если
Задача 1. Найти объем пирамиды АВСD, если А (1; 1; -1), В (2; 1; 0), С (3; 2; -1), D (-1; 2; 1).
Задача 2. Векторы
Решение.
 
Задача 3. Даны 3 вектора Найти значение «l», при котором: 1) векторы 2) 3) 4) 5) 6) Векторы Решение: Находим смешанное произведение векторов
1) Если 2) Если 3) 4) 5)
6) Если тройка векторов левая, то их смешанное произведение отрицательно, а поскольку Решить самостоятельно: 1) Даны вершины пирамиды АВСD: А (1; 2; -3), В (2; 2; -2), С (2; 1; -4), D (-2; -2; -1). Найти а) объем пирамиды, б) длину высоты, опущенной на основание АВС. 2) Даны 3 вектора: 2.1.) векторы 2.2.) 2.3.) 2.4.) 2.5.) 2.6.)
|

 .
.
 3) Смешанное произведение ненулевых векторов равно нулю
3) Смешанное произведение ненулевых векторов равно нулю 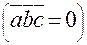 тогда и только тогда, когда сомножители компланарны.
тогда и только тогда, когда сомножители компланарны. численно равен объему параллелепипеда, построенного на этих векторах, как на ребрах:
численно равен объему параллелепипеда, построенного на этих векторах, как на ребрах:

 > 0, то векторы образуют правую тройку, если
> 0, то векторы образуют правую тройку, если  ,
,  ,
, 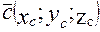 , то их смешанное произведение вычисляется по формуле:
, то их смешанное произведение вычисляется по формуле: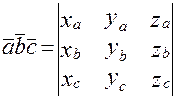
 ,
,  ,
, 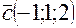 , то
, то
 Решение.
Решение.


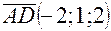

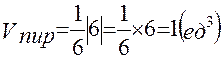 .
. ,
,  ,
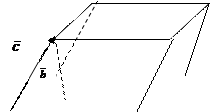
, 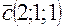 являются ребрами параллелепипеда. Найти длину высоты параллелепипеда, опущенной на грань векторов
являются ребрами параллелепипеда. Найти длину высоты параллелепипеда, опущенной на грань векторов  и
и  .
.


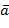
 . С другой стороны
. С другой стороны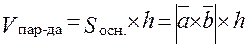 , следовательно
, следовательно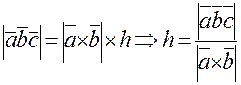





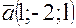 ,
,  ,
, 

 компланарны;
компланарны;


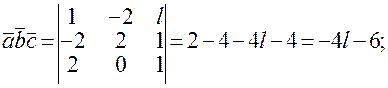




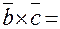


 , то для левой тройки
, то для левой тройки 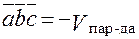 , следовательно в нашей задаче
, следовательно в нашей задаче 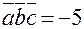 , т.е.
, т.е. 
 ,
,  ,
,  . Найти значения «m», при которых:
. Найти значения «m», при которых:





