Плоскость и прямая в пространстве

Плоскость в декартовой прямоугольной системе координат Oxyz может быть задана уравнением одного из следующих видов: 1) 2) A 3) Угол ß между двумя плоскостями

Находится как угол между их векторами нормалей
Условие параллельности двух плоскостей:
Условие перпендикулярности двух плоскостей:
Пример 1. Уравнение плоскости, проходящей через точку А (3; -1; 2) перпендикулярно вектору Пример 2. Уравнение плоскости, проходящей через точки
Пример3. Угол между плоскостями
Прямая в пространстве может быть задана одним из следующих уравнений: 1) Эта прямая проходит через заданную точку 2) 3)
 - уравнение прямой, заданной как пересечение двух плоскостей. - уравнение прямой, заданной как пересечение двух плоскостей.
Пусть заданы две прямые:
Угол ß между двумя прямыми в пространстве находится как угол между их направляющими векторами
Условие параллельности двух прямых в пространстве:
Условие перпендикулярности двух прямых:
Пример 1. Составить уравнение прямой, проходящей через точку Решение. У заданной прямой направляющий вектор
Пример 2. Написать параметрическое уравнение прямой, проходящей через точки Решение. Составляем уравнение прямой по формуле (3):
Пример 3. Записать в каноническом виде уравнение прямой, заданной как пересечение плоскостей:
Решение. Чтобы записать уравнение прямой в каноническом виде, надо найти направляющий вектор этой прямой и какую-либо точку этой прямой. Найти точку- это значит найти какое-либо решение системы уравнений. Положим z = 0, тогда
 Поскольку направляющий вектор Поскольку направляющий вектор 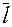
перпендикулярен к векторам нормалей обеих плоскостей, его можно получить как векторное произведение векторов нормалей
Уравнение прямой l имеет вид:
|

 - общее уравнение плоскости, в котором коэффициенты А, В, С являются координатами вектора нормали:
- общее уравнение плоскости, в котором коэффициенты А, В, С являются координатами вектора нормали:  .
. - уравнение плоскости, проходящей через точку
- уравнение плоскости, проходящей через точку  перпендикулярно вектору
перпендикулярно вектору  - уравнение плоскости, проходящей через три заданные точки:
- уравнение плоскости, проходящей через три заданные точки:  ,
,  ,
, 




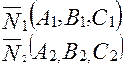 и
и
 , (т.е.
, (т.е.  ║
║  )
) , (т.е.
, (т.е.  , поскольку
, поскольку  )
) (2; -2; 1) имеет вид:
(2; -2; 1) имеет вид:  , т.е.
, т.е. 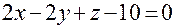 (уравнение (2)).
(уравнение (2)). ,
, 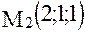 ,
,  имеет вид (уравнение (3)):
имеет вид (уравнение (3)): , т.е.
, т.е. 
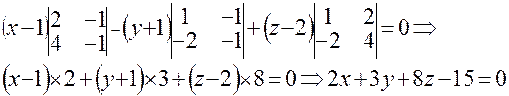
 и
и 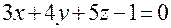 найдется по формуле (4):
найдется по формуле (4):

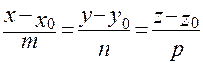 - канонические уравнения прямой.
- канонические уравнения прямой. .
. - уравнение прямой в параметрическом виде.
- уравнение прямой в параметрическом виде.
 - уравнение прямой, прохлдящей через две заданные точки
- уравнение прямой, прохлдящей через две заданные точки 



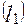 и
и

 и
и  :
: (5)
(5) (т.е.
(т.е.  ║
║  )
) (т.е.
(т.е. 

 параллельно прямой
параллельно прямой 
 . Поскольку искомая прямая ей параллельна, то вектор
. Поскольку искомая прямая ей параллельна, то вектор 
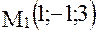 и
и  .
.
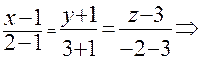
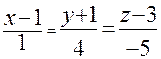 . Получили уравнение прямой в каноническом виде. Чтобы привести его к параметрическому виду, приравниваем его к t:
. Получили уравнение прямой в каноническом виде. Чтобы привести его к параметрическому виду, приравниваем его к t:

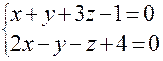

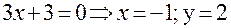 , получим точку
, получим точку  .
.

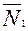
 и
и 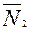
 .
. , т.е.
, т.е. 




