Окружности
Уравнение Например, уравнение Если центр окружности совпадает с началом координат, то уравнение принимает вид Задача 1. Составить уравнение окружности, для которой точки А(5; 2) и В(-3; 4) являются концами одного диаметра. Решение. Чтобы записать уравнение окружности, надо найти ее центр и радиус. Поскольку точки А и В являются концами одного диаметра, то центром окружности будет середина отрезка АВ, поэтому
Радиус окружности равен длине вектора
Задача 2. Найти центр и радиус окружности:
Решение. Заданное уравнение надо привести к виду Для этого группируем члены, содержащие x и y и выделяем полные квадраты:
Эллипсом называется геометрическое место точек, для которых сумма расстояний от двух заданных точек, называемых фокусами, есть величина постоянная, равная 2a:
Каноническое уравнение эллипса имеет вид:
Величина Задача. Составить уравнение эллипса по следующим данным: 1) большая ось равна 10, межфокусное расстояние =8; 2) межфокусное расстояние = 6, а 3) большая полуось = 4, а точка М(2; -2) лежит на эллипсе. Решение. Чтобы записать уравнение эллипса, надо найти его полуоси a и b. 1)
2)
3)
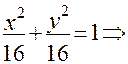 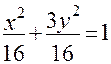

Гиперболой называется геометрическое место точек, для которых разность расстояний от двух заданных точек, называемых фокусами, есть величина постоянная: Каноническое уравнение гиперболы имеет вид:
Эксцентриситет гиперболы Две прямые Задача. Составить уравнение гиперболы по следующим данным: 1) действительная полуось 2) 3) Решение. 1)
2)
4) точка М(12; 3
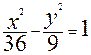 - уравнение гиперболы. - уравнение гиперболы.
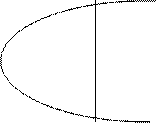
  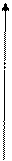 Парабола. Парабола.
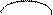
Параболой называется геометрическое место точек, равноудаленных от заданной точки, называемой фокусом, и от заданной прямой, называемой директрисой: MF=MN, где фокус F Каноническое уравнение параболы имеет вид: Задача 1. Найти точки с абсциссой Решение. Фокус параболы находится в точке F Задача 2. Через фокус параболы Решение.
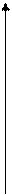 Парабола расположена в системе координат каноническим способом. Парабола расположена в системе координат каноническим способом.
|

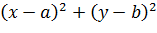 =
= 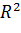 определяет окружность радиуса R с центром в точке С (a, b).
определяет окружность радиуса R с центром в точке С (a, b).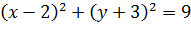 определяет окружность радиуса R=3 c центром в точке С (2; -3).
определяет окружность радиуса R=3 c центром в точке С (2; -3).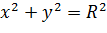
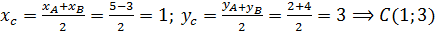
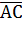 :
: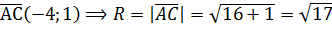 . Уравнение окружности:
. Уравнение окружности: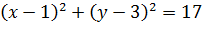
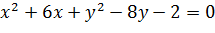
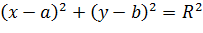 .
.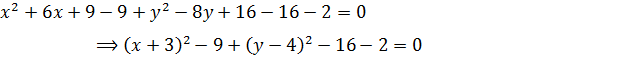
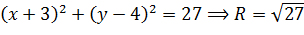 , а центр – С (-3; 4).
, а центр – С (-3; 4). ллипс.
ллипс.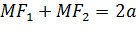 , где
, где 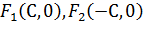 - фокусы эллипса.
- фокусы эллипса.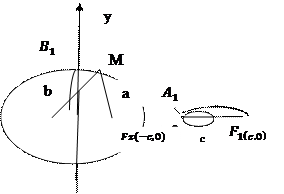

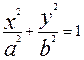 , где
, где 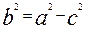 ,
, 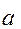 - большая полуось,
- большая полуось, 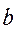 -
-  малая полуось.
малая полуось.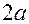 - большая ось (
- большая ось ( ),
), 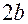 - малая ось (
- малая ось (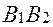 )
)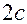 - межфокусное расстояние (
- межфокусное расстояние (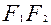 )
)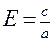 - эксцентриситет эллипса; E< 1.
- эксцентриситет эллипса; E< 1.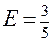 ;
;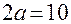 ;
; 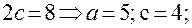 по формуле
по формуле 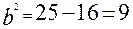 . Уравнение эллипса имеет вид:
. Уравнение эллипса имеет вид: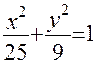
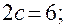
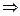
 , а поскольку
, а поскольку 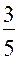 =
= 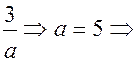
 . Уравнение эллипса имеет вид
. Уравнение эллипса имеет вид 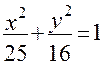
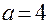 , а поскольку точка М(2; -2) лежит на эллипсе, ее координаты удовлетворяют уравнению
, а поскольку точка М(2; -2) лежит на эллипсе, ее координаты удовлетворяют уравнению 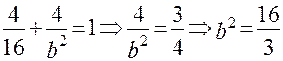 . Уравнение эллипса
. Уравнение эллипса
 Гипербола.
Гипербола.
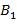
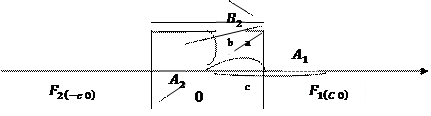
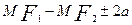 , где
, где 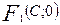 и
и 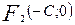 - фокусы гиперболы.
- фокусы гиперболы.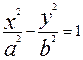 , где
, где 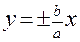 (диагонали прямоугольника со сторонами
(диагонали прямоугольника со сторонами 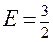 ;
;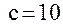 , а прямые
, а прямые 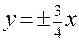 являются асимптотами;
являются асимптотами;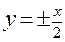 - асимптоты, а точка М(12; 3
- асимптоты, а точка М(12; 3 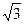 ) лежит на гиперболе.
) лежит на гиперболе. ; по формуле
; по формуле 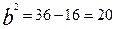
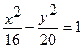 - уравнение гиперболы.
- уравнение гиперболы.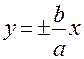 , поэтому имеем
, поэтому имеем 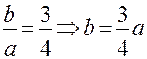 . по формуле
. по формуле 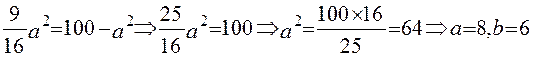
 - уравнение гиперболы.
- уравнение гиперболы.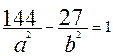 ,
, 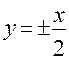 - асимптоты, а значит
- асимптоты, а значит 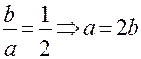 . Подставляя
. Подставляя 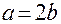 в первое уравнение, получаем:
в первое уравнение, получаем: 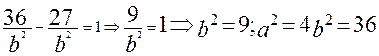
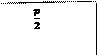

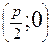 , x =
, x = 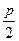 - директриса.
- директриса.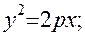
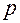 - параметр параболы.
- параметр параболы.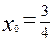 на параболе, фокус которой находится в точке F
на параболе, фокус которой находится в точке F 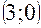 , а вершина – в начале координат.
, а вершина – в начале координат.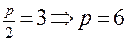 и уравнение параболы имеет вид:
и уравнение параболы имеет вид: 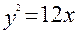 . Точки с абсциссой
. Точки с абсциссой 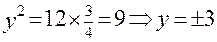 . Получим две точки:
. Получим две точки: 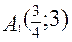 и
и 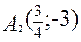 .
.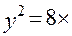 проведена хорда, перпендикулярная к ее оси. Определите длину этой хорды.
проведена хорда, перпендикулярная к ее оси. Определите длину этой хорды.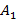
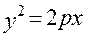 , следовательно, в данной задаче
, следовательно, в данной задаче 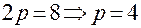 , а значит фокус имеет координаты F
, а значит фокус имеет координаты F  . Найдем ординаты точек
. Найдем ординаты точек  и
и 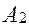 :
: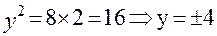 , следовательно,
, следовательно, 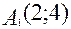 ,
, 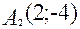 . Длина хорды
. Длина хорды 


