Производные высших порядков. Пусть функция y=f(x) имеет производную y'=f'(x) в каждой точке некоторого промежутка
Пусть функция y=f(x) имеет производную y'=f'(x) в каждой точке некоторого промежутка. Эта производная в общем случае сама является функцией от x и может быть продифференцирована. Производную от производной y'=f'(x) называют производной второго порядка (или второй производной) и обозначают одним из символов:
Дифференцируя производную второго порядка, получаем производную третьего порядка Для ее обозначения, применяют символы:
Если функция y от x задана параметрически: То ее производные любых порядков находят последовательно по формулам:
Пример 1. Найти производную 4-го порядка
Пример 2. Функция y от x задана параметрически: Найти производную 3-го порядка
6.5. Правило Лопиталя. Правилом Лопиталя называют следующее общее правило для раскрытия неопределенностей вида Если функции f(x) и φ (x) удовлетворяют условиям: 1) 2)В некоторой окрестности точки 3)Существует конечный или бесконечный Другие виды неопределенностей (0 Пример 1. Найти Решение.
Пример 1. Найти Решение.
Решить самостоятельно. Вычислить пределы. 1) 1) 7)
|


 ;
;  ;
; 
 , затем
, затем  ,
,  и т.д. Производной n-ого порядка функции y=f(x) называется производная от производной
и т.д. Производной n-ого порядка функции y=f(x) называется производная от производной  -го порядка.
-го порядка.
 ;
;  ;
; 

 ;
;  ;
;  и т.д.
и т.д.
 .
.



 ;
; 
 =
= 
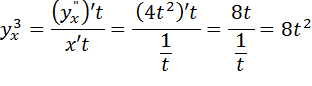
 и
и 
 или
или 
 , за исключением, быть может, самой точки
, за исключением, быть может, самой точки  ;
; , то
, то 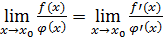
 с помощью алгебраических преобразований или логарифмирования сводятся к неопределенностям вида
с помощью алгебраических преобразований или логарифмирования сводятся к неопределенностям вида 




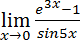 ; 2)
; 2)  ; 3)
; 3) 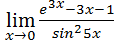
 5)
5)  ; 6)
; 6) 
 ; 8)
; 8)  ; 9)
; 9) 



